Пусть дана точка 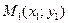 . Так как нам необходимо составить уравнение прямой, то оно будет иметь вид
. Так как нам необходимо составить уравнение прямой, то оно будет иметь вид 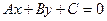 . Поскольку точка
. Поскольку точка 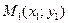 принадлежит этой прямой, то ее координаты удовлетворяют общему уравнению прямой:
принадлежит этой прямой, то ее координаты удовлетворяют общему уравнению прямой: 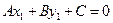 . Вычтя из предыдущего уравнения данное и выполнив простейшие преобразования, мы имеем:
. Вычтя из предыдущего уравнения данное и выполнив простейшие преобразования, мы имеем: 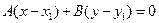 . При любом
. При любом 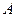 и
и 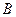 этому уравнению удовлетворяют координаты точки
этому уравнению удовлетворяют координаты точки 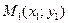 .
.
Таким образом: 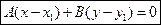 – уравнение прямой, проходящей через данную точку с координатами
– уравнение прямой, проходящей через данную точку с координатами 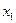 и
и 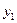 .
.
3.9. Уравнение прямой, проходящей через две данные (различные) точки 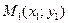 и
и 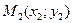
Уравнение прямой проходящей через 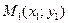 имеет вид:
имеет вид: 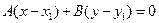 или
или 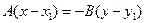 . Применив свойство пропорции, имеем:
. Применив свойство пропорции, имеем: 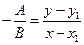 .
.
Так как искомая прямая проходит и через точку 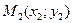 , то ее уравнение:
, то ее уравнение: 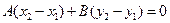 или
или 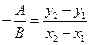 . Имеем:
. Имеем: 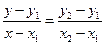 или
или 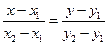 .
.
 2015-06-28
2015-06-28 1187
1187
