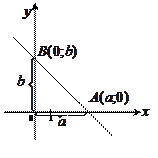 Пусть дана прямая
Пусть дана прямая 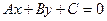 . Если
. Если 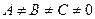 , то, разделив на
, то, разделив на 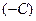 . Имеем:
. Имеем: 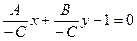 , или
, или 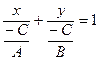 . Обозначив
. Обозначив 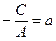 ,
, 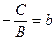 , получим
, получим 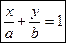 – уравнение прямой в отрезках;
– уравнение прямой в отрезках; 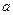 и
и 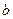 – отрезки, которые она отсекает на осях координат.
– отрезки, которые она отсекает на осях координат.
3.7. Уравнение прямой, проходящей через данную точку
в данном направлении
Пусть дана точка 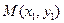 . Выведем уравнение прямой, проходящей через нее и имеющей угловой коэффициент
. Выведем уравнение прямой, проходящей через нее и имеющей угловой коэффициент 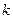 . Искомое уравнение должно иметь вид
. Искомое уравнение должно иметь вид 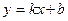 , но т.к. прямая проходит через
, но т.к. прямая проходит через 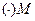 , то ее координаты удовлетворяют данному уравнению:
, то ее координаты удовлетворяют данному уравнению: 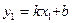 . Если мы из первого уравнения вычтем почленно второе, то
. Если мы из первого уравнения вычтем почленно второе, то 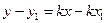
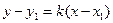 . Это и есть искомое уравнение:
. Это и есть искомое уравнение: 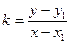 ;
; 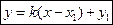 .
.
 2015-06-28
2015-06-28 605
605








