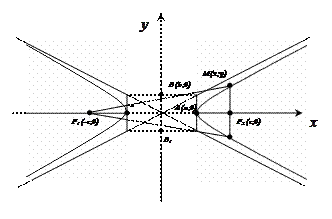
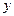 Определение: гиперболой называется геометрическое место точек плоскости, разность расстояний каждой из которых до двух данных точек
Определение: гиперболой называется геометрическое место точек плоскости, разность расстояний каждой из которых до двух данных точек 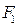 и
и 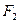 (называемых фокусами) есть величина постоянная, равная
(называемых фокусами) есть величина постоянная, равная 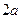 . Обозначим через
. Обозначим через 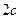 расстояние
расстояние 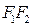 .
.
|
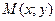 – произвольная точка гиперболы. Для построения гиперболы надо построить ее основной прямоугольник со сторонами
– произвольная точка гиперболы. Для построения гиперболы надо построить ее основной прямоугольник со сторонами 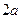 и
и 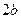 и центром в начале координат. Тогда по определению гиперболы
и центром в начале координат. Тогда по определению гиперболы 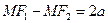 .
. 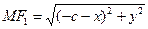 ,
,
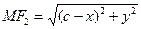 , т.е.
, т.е. 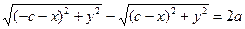 –уравнение гиперболы.
–уравнение гиперболы.
1) Канонический вид уравнения: 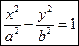 .
.
2) Гипербола симметрична относительно осей координат. Она имеет две ветви. 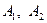 – ее вершины.
– ее вершины.
3) Если 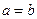 , то гипербола равностороння (равнобочная) и ее уравнение
, то гипербола равностороння (равнобочная) и ее уравнение 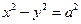 .
.
4) Прямые 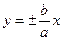 – асимптоты гиперболы. У равнобочной гиперболы асимптоты перпендикулярны.
– асимптоты гиперболы. У равнобочной гиперболы асимптоты перпендикулярны.
5) Эксцентриситет гиперболы 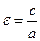 ,
, 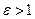 , т.к.
, т.к. 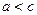 . Гипербола
. Гипербола 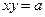 , где
, где 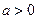 – равностороння гипербола, имеющая своими асимптотами оси координат.
– равностороння гипербола, имеющая своими асимптотами оси координат.




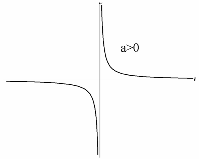
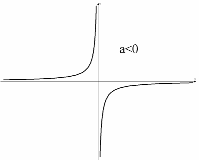
6) Параметры гиперболы – 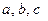 и
и 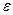 .
.
 2015-06-28
2015-06-28 4747
4747