Маємо: x = 
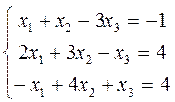
1) Знайти А=I-x (xТx)-1 xТ
2) Довести, що матриця ідемпотентна і знайти ранг А.
3) Навести квадратичну форму zТAz до канонічного вигляду, знайти 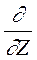
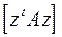
4) Розв¢язати методом жорданових виключень систему рівнянь.
РОЗВ¢ЯЗАННЯ:
1) Обчислимо А.
Xtx = 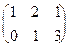
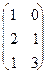 =
= 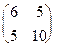
Знайдемо методом жорданових виключень (хtx)-1.
| x1 | x2 | |
| У | [6] | |
| У2 |
ß
| y1 | x2 | ||
| x1 | [1] | -5 | :6 |
| y2 |
| y1 | x2 | y1 | y2 | y1 | y2 | ||||||
| x1 | 1/6 | -5/6 | Þ | x1 | 10/6 | -5/6 | :35/6 | Þ | x1 | 10/35 | -5/35 |
| y2 | 5/6 | [35/6] | x2 | -5/6. | [1] | x2 | -5/35 | -6/35 |
Отримали (xtx)-1= 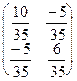 =
= 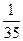
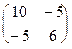
Перевіримо правильність обчислення:
I=(xtx)-1*(xtx)= 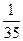
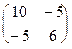
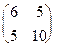 =
= 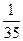
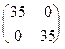 =
= 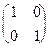
Отже, обернена матриця знайдена вірно.
Обчислимо x(xtx)-1xt
x(xtx)-1 = 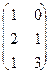
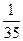
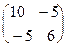 =
= 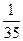
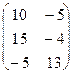
x(xtx)-1xt = 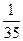
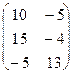
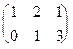 =
= 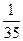
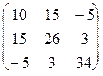
Тоді маємо:
A=I- x(xtx)-1xt= 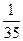
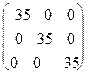 -
- 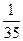
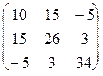 =
= 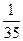
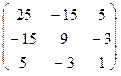
2). Доведемо, що А ідемпотентна, тобто А х А =А
А х А= 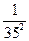
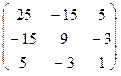
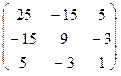 =
= 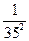
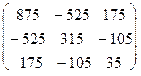 =
=
= 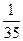
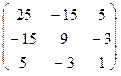 =А
=А
Методом жорданових виключень знайдемо ранг А.
| х1 | х2 | х3 | х1 | х2 | y3 | ||||
| у1 | -15 | у1 | : 1 | ||||||
| у2 | -15 | -3 | Þ | у2 | -3 | ||||
| у3 | -3 | [1] | x3 | -5 |
Тоді ранг А=1
3) Наведемо квадратичну форму ztAz до канонічного вигляду.
Не канонічний вигляд:
(z1z2z3) 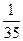
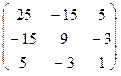
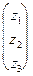 =
= 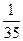 (z1z2z3)
(z1z2z3) 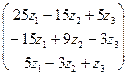 =
= 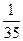 [25z12-
[25z12-
-15z1z2+5z1z3-15z1z2+9z22-3z2z3+5z1z3-3z2z3+z32]= 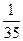 [25z12+9z22+z32+2(-15 z1z2+5z1z3--3z2z3)]
[25z12+9z22+z32+2(-15 z1z2+5z1z3--3z2z3)]
Так як матриця А симетрична, тобто Ат=А, то існує така ортогональна матриця Q, що QtAQ=l= 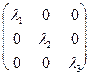 , li (і =
, li (і = 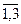 ) - власні значення матриці А, рішення характеристичного рівняння |A-lI| = 0. Матриця Q складається з власних векторів матриці А, які є рішеннямb матричного рівняння А
) - власні значення матриці А, рішення характеристичного рівняння |A-lI| = 0. Матриця Q складається з власних векторів матриці А, які є рішеннямb матричного рівняння А 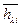 = li
= li 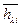 (і =
(і = 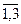 ),
),
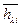 =
= 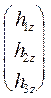
Розв¢яжемо характеристичне рівняння.
|A-lI| = 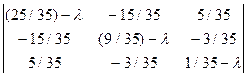 =
= 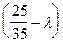
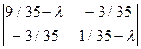 +
+
+ 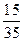
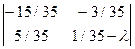 +
+ 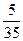
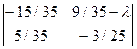 =
= 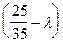
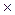
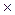
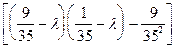 + 15/35
+ 15/35 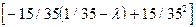 +
+
+ 5/35 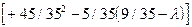 = (25/35-l)(+l2-10l/35)+15/35*15l/35+
= (25/35-l)(+l2-10l/35)+15/35*15l/35+
+5/35(5l/35) = -l3+l2=0
l2(-l+1)=0 Þ l1=1; l2,3=0
Знайдемо власні вектори 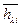 , які відповідають власним значенням lі.
, які відповідають власним значенням lі.
l1=1
[A-lіI] 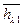 =0 [A-I]
=0 [A-I] 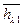 = 0
= 0
1/35 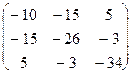
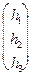 = 0 Þ
= 0 Þ 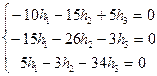 Þ
Þ
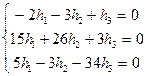
Розв¢яжемо систему методом виключень, виключимо h3 з другого і третього рівнянь.
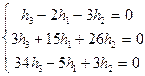 Þ
Þ 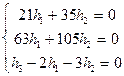 Þ
Þ 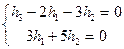
h2=3k, 3h1=-5(3k), h1=-5k, h3=2h1+3h2=2(-5k)+3*3k=-k
Отримали 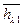 =
= 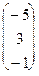 к. Пронормуємо
к. Пронормуємо 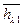 , тобто ½
, тобто ½ 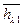 ½2=1 Þ
½2=1 Þ
к2(25+9+1)=1 к = 1/ 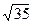
Тоді 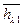 =1/
=1/ 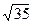
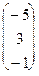
l2=0 [A] 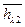 =0 Þ
=0 Þ 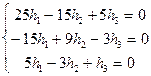 Þ 5h1-3h2+h3=0
Þ 5h1-3h2+h3=0
h3=-5h1+3h2 ì h1=0; h2=k; h3=3k Þ 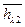 =k
=k 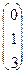 ï
ï 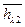 ï2=1 Þ (02+12+32)k2=1
ï2=1 Þ (02+12+32)k2=1
k=1/ 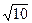
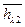 = 1/
= 1/ 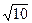
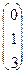
l3=0
За умови ортогональності 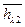
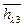 = 0. Якщо
= 0. Якщо 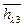 =
= 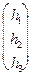 , то
, то
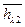 *
* 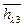 =1/
=1/ 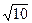 (0*h1+h2+3h3)=0
(0*h1+h2+3h3)=0
Тоді
é 5h1-3h2+h3=0
ë 0*h1+h2+3h3=0 Þ h3=k, h2=-3k, 5h1=-10k, h1=-2k
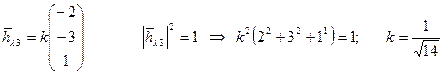
Отримаємо: 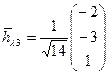
Тоді ортогональна матриця 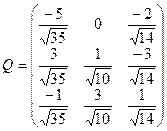
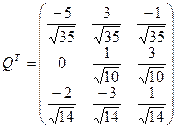
Перевіримо правильність обчислень
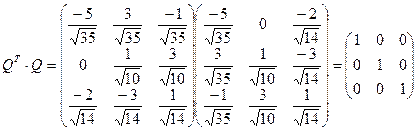
Проведемо заміну змінних 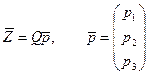
Тоді 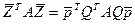
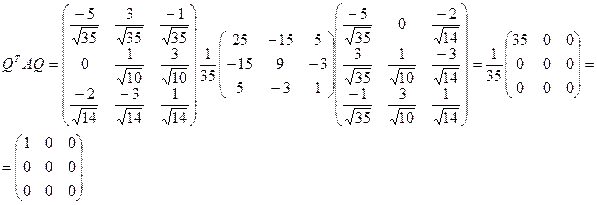
Приведемо форму до канонічного вигляду:
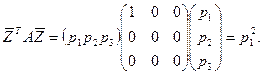
де 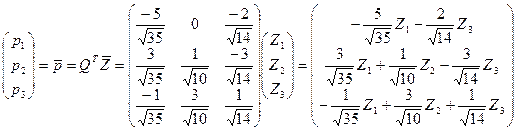

Знайдемо 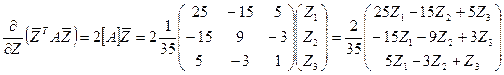
Розв'яжемо систему лінійних рівнянь з правою частиною методом жорданових включень, її матричний вигляд 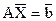 , запишемо данні в жорданову таблицю.
, запишемо данні в жорданову таблицю.
| x1 | x2 | x3 | y1 | x2 | x3 | ||||||
| y1 | [1] | -3 | Þ | x1 | [1] | -1 | -1 | : 1 Þ | |||
| y2 | -1 | -1 | -4 | y2 | -6 | ||||||
| y3 | -1 | -4 | y3 | -1 | -2 | -3 |
| x1 | x2 | x3 | |||
| Þ | y1 | [1] | -3 | ||
| y2 | -1 | -1 | -4 | ||
| y3 | -1 | -4 |
В результаті 1-го кроку ми змінили місцями x1 і y1, x1 стала залежною, а y1 - незалежною змінною. Далі змінюємо x2 на y2, обираючи а22=1 розв'язувальним елементом.
| y1 | x2 | x3 | y1 | y2 | x3 | |||||
| x1 | -1 | -7 | :1Þ | x1 | -1 | -7 | ||||
| x2 | -2 | [1] | -5 | x2 | -2 | -5 | ||||
| y3 | -27 | y3 | [27] |
На третьому кроці змінюємо x3 на y3, обираючи розв'язувальним елементом а33=-27.
| y1 | y2 | x3 | y1 | y2 | y3 | |||||
| x1 | -13 | -27 | :-27Þ | x1 | -7/27 | 13/27 | -8/27 | |||
| x2 | -1 | -2 | -5 | -27 | x2 | 1/27 | 2/27 | 5/27 | ||
| y3 | -5 | [1] | -27 | x3 | -11/27 | 5/27 | -1/27 |
Отримали рішення системи при y1=y2=y3=0; x1=x2=x3=1 і обернену
матрицю системи рівнянь.
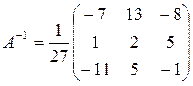
Перевіримо отриманий результат
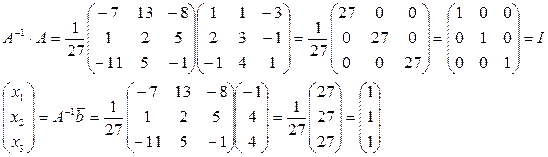
Тоді рішення вірно.
 2015-06-28
2015-06-28 360
360








