Розв’язування загальної системи лінійних рівнянь

Розглянемо систему m лінійних рівнянь з n змінними:

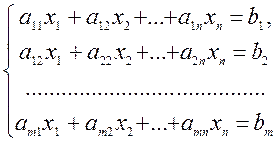
Позначимо через [A] матрицю системи, через [C] - розширену матрицю, тобто матрицю [A] з приєднаним справа стовпцем рівних членів. Очевидно, що rang [C] розширеної матриці або дорівнює рангу матриці [A ], або на одиницю більший.

Теорема Кронекора-Капеллі. Система m лінійних рівнянь з n незалежними змінними сумісна тоді, коли ранг матриці [A] дорівнює рангу розширеної матриці [C]. Якщо ранг розширеної матриці дорівнює рангу матриці [A] і числу невідомих, тобто rang [А] = rang [C] =n, то система має єдиний розв’язок. Якщо ранг матриці менший, ніж число невідомих (rang [А] = rang [C] < n), то система рівнянь має безліч розв’язків.

Якщо ранг матриці [A] не дорівнює рангу матриці [C], то система лінійних рівнянь несумісна.

Розв’яжемо загальну систему лінійних рівнянь методом ЗЖВ. Припустимо, що умова Кронекера - Капеллі виконується:

rang [А] = rang [C] = k < n.

Перепишемо систему рівнянь у вигляді

.

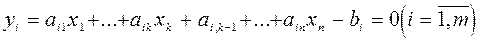Подамо цю систему у вигляді жорданової таблиці:

	x1	...	xk	xk+1	...	xn
y1	a11	...	a1k	a1,k+1	...	a1n	-b1
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
yk	ak1	...	akk	ak,k+1	...	akn	-bk
yk-1	ak+1	...	ak+1,k	ak+1,k+1	...	ak+1,n	-bk+1
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
ym	am1	...	amk	am,k+1	...	amn	-bm

Оскільки rang [А] = rang [C] = k, то над цією таблицею можна послідовно виконати k кроків ЗВЖ. Не порушуючи загальності, можна вважити, що в результаті k кроків ЗВЖ ми змінили перші залежні змінні 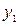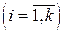на перші незалежні змінні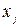 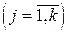. Після k кроків таблиця набуває вигляду:

	y1	...	yk	xk+1	...	xn
x1		...			...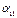
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
...	...	...	...	...	...	...	...
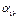
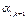
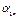
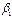
xk		...			...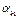
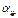
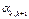
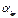
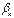
yk+1		...			...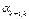
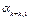
ym		...			...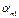

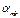
Загальний розв’язок має вигляд:

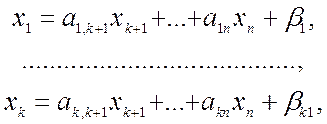
Залежні змінні 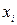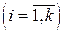називають базисними, а весь набір х₁,..., х_к базисом системи змінних х_j 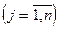. Незалежні змінні 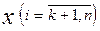у загальному розв'язку системи називають вільними змінними. Якщо вільним змінним надати певних значень x_k+1= 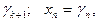то дістанемо частинний розв'язок системи:

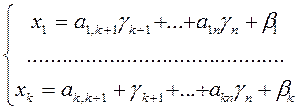
Оскільки вільним змінним можна надавати довільних значень, то система має нескінченну множину розв'язків.

Частинний розв'язок системи рівнянь, в якому вільним змінним надається значення, що дорівнює нулю,називається базисним:

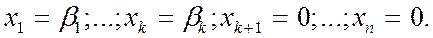
Базисними можуть бути будь-які k із n змінних. Відомо, що число різних підмножин із k елементів, складених із множини n змінних, дорівнює числу комбінацій із n елементів по k, тобто

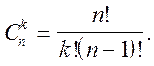
Насправді базисних розв'язиків може виявитися менше,оскільки деякі з визначників k-го порядку, складених із елементів, що розміщені на перетині k різних рядків та k різних стовпців, можуть дорівнювати нулю. Залежні змінні у_k+1,...,у_m виражаються лінійно через решту :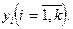

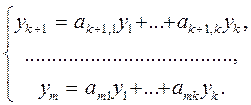
Приклад

Знайти загальний розв'язок системи рівнянь

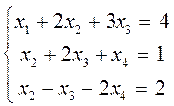
Перепишемо систему у такому вигляді:

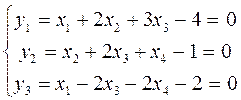
Тепер подамо її у табличній формі:

	x1	x2	x3	x4
y1					-4
y2					-1
y3			-1	-2	-2

Над отриманою таблицею послідовно виконаємо максимально можливе число кроків ЗЖВ, беручи кожний рядок і кожен стовпець як рoзв'язувальний не більше одного разу:

	y1	x2	x3	x4
x1		-2	-3
y2					-1
y3		-2	-4	-2

	y1	y2	x3	x4
x1		-2
x2			-2	-1
y3		-2

Із таблиці випливає, що rang[A]=rang[C]=2, оскільи вгору "перекинули" лише дві змінні, а вільний член у третьому рядку дорівнює нулю. Система має такий розв'язок:

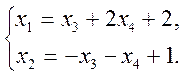
Якщо надати х₃ та х₄ певних сталих значень, то дістанемо частинний розв'язок..