2015-06-28
418
Розглянемо невироджену матрицю n-го порядку:
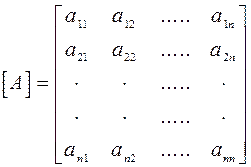
Для визначення оберненої матриці складемо систему лінійних рівнянь, в якій роль вільних членів виконуватимуть залежні змінні:
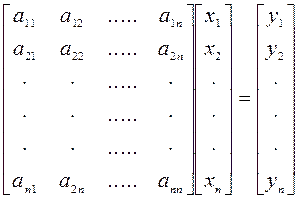
або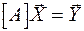 
.
Припустимо, що треба знайти розв'язок системи. Помножимо обидві частини рівності на обернену матрицю:
.
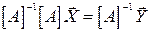Враховуючи, що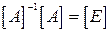 
, а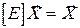 
, дістанемо 
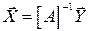.Відшукання оберненої матриці зводиться до того, щоб незалежні змінні xi 
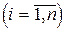зробити залежними і залежні змінні yj 
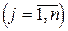зробити незалежними.
Запишемо систему рівнянь у табличній формі:
| x1 | x2 | .... | xn | |
| y1 | a11 | a12 | .... | a1n |
| y2 | a21 | a22 | .... | a2n |
| · | · | · | .... | · |
| · | · | · | .... | · |
| yn | an1 | an2 | .... | ann |
Щоб поміняти незалежні змінні на залежні і навпаки, послідовно виконаємо над таблицею n кроків ЗЖВ. Якщо за розв'язувальні брати не лише діагональні елементи, то після перестановки деяких рядків та деяких стовпців таблиця набуде вигляду:
| y1 | y2 | .... | yn | |
| x1 | a11 | a12 | .... | a1n |
| x2 | a21 | a22 | .... | a2n |
| · | · | · | .... | . |
| · | · | · | .... | . |
| xn | an1 | an2 | .... | ann |
Матриця цієї таблиці є оберненою до матриці [A], тобто
|
|
|
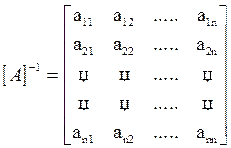
Приклад
Нехай задана вироджена матриця:
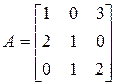
Знайти матрицю, обернену до матриці [A]. Складемо таблицю:
| x1 | x2 | x3 | |
| y1 | [1] | ||
| y2 | |||
| y3 |
Зробивши один крок ЗЖВ з розв'язувальним елементом а11=1, дістанемо таблицю:
| y1 | x2 | x3 | |
| x1 | -3 | ||
| y2 | [1] | -6 | |
| y3 |
Другий крок ЗЖВ зробимо з розв'язувальним елементом а22=1:
| y1 | y2 | x3 | |
| x1 | -3 | ||
| x2 | -2 | ||
| y3 | -2 | [8] |
| :8 Þ |
| y1 | y2 | y3 | |
| x1 | 1/4 | 3/8 | -3/8 |
| x2 | -1/2 | 1/4 | 3/4 |
| x3 | 1/4 | -1/8 | 1/8 |
Третій крок ЗЖВ можна зробити лише з розв'язувальним елементом а33=8:
| y1 | y2 | y3 | |
| x1 | -3 | ||
| x2 | -4 | ||
| x3 | -1 |
Обернена матриця має вигляд:
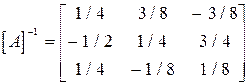
У даному прикладі не було необхідності переставляти рядки та стовпці, оскільки за розв'язувальні вибрали діагональні елементи.
