ТЕОРИЯ ИГР
ДУБЛИРОВАНИЕ И ДОМИНИРОВАНИЕ СТРАТЕГИЙ
Дублирование стратегий – из одинаковых строк (столбцов) оставляем одну (один).
Доминирование стратегий – если одна строка поэлементно больше либо равна другой, удаляем меньшую. Это же правило (со знаком 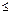 ) применяем к столбцам. (Если игра ) применяем к столбцам. (Если игра 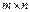 имеет седловую точку, то после всех описанных преобразований получим игру имеет седловую точку, то после всех описанных преобразований получим игру 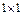 ).
СВЕДЕНИЕ МАТРИЧНОЙ ИГРЫ К ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ).
СВЕДЕНИЕ МАТРИЧНОЙ ИГРЫ К ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Припишем строкам вероятности
Вводя новые переменные
Аналогично,приписывая столбцам матрицы вероятности
Любую из этих задач можно решить одним из алгоритмов симплекс-метода, а затем, на основание теории двойственности, найти решение другой задачи.
| ПРИМЕРЫ
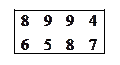 4.Дублирование и доминирование стратегий 4.Дублирование и доминирование стратегий
 Упростим игру. 4-я строка дублирует первую. Вторая строка доминирует над третьей. Оставшиеся две строки несравнимы Упростим игру. 4-я строка дублирует первую. Вторая строка доминирует над третьей. Оставшиеся две строки несравнимы
 Получим матрицу. Второй столбец доминирует над третьим. Оставшиеся строки и столбцы несравнимы. Таким образом, игру Получим матрицу. Второй столбец доминирует над третьим. Оставшиеся строки и столбцы несравнимы. Таким образом, игру 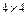 свели к игре свели к игре 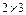 5.Графический способ решения игр
5.Графический способ решения игр 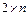 и и 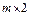
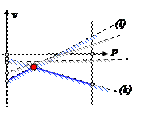
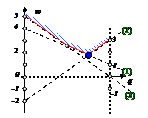
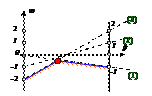 Игра Игра 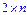 :Приписав 1-й строке вероятность p, а 2-й – вероятность (1- p), получим n линейных сооношений, по графикам которых выберем их нижнюю огибающую. Максимум этой огибающей даст нам точку, координатами которой являются: значения вероятности p и цены игры v. Пусть эта точка является пересечением i-й и j-й прямых. Приписываем i-му столбцу вероятность q, а j-му столбцу – вероятность (1- q). Из получившейся системы уравнений находим q и (1- q).Найдем решение матричной игры: :Приписав 1-й строке вероятность p, а 2-й – вероятность (1- p), получим n линейных сооношений, по графикам которых выберем их нижнюю огибающую. Максимум этой огибающей даст нам точку, координатами которой являются: значения вероятности p и цены игры v. Пусть эта точка является пересечением i-й и j-й прямых. Приписываем i-му столбцу вероятность q, а j-му столбцу – вероятность (1- q). Из получившейся системы уравнений находим q и (1- q).Найдем решение матричной игры:
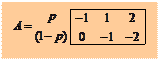 Решая уравнения (1) и(3) получаем p =2/5, (1- p) =3/5 и v = w(2/5)= –2/5.
Оптимальная стратегия игрока А:
Решая уравнения (1) и(3) получаем p =2/5, (1- p) =3/5 и v = w(2/5)= –2/5.
Оптимальная стратегия игрока А: 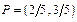 . Цена игры (выигрыш) – v = –2/5.
Первому столбцу припишем ненулевую вероятность q, а третьему – (1- q). Второму столбцу будет соответствовать нулевая вероятность. Решая систему . Цена игры (выигрыш) – v = –2/5.
Первому столбцу припишем ненулевую вероятность q, а третьему – (1- q). Второму столбцу будет соответствовать нулевая вероятность. Решая систему
находим q = 4/5 и (1- q) = 1/5. Оптимальная стратегия игрока В:
Ненулевые вероятности p и (1-p) припишем 1-й и 2-й строке. Решая полученную систему, находим p =5/8, (1- q) =3/8 Оптимальные стратегии: Игрок А – Игрок В – |
 2015-06-28
2015-06-28 703
703
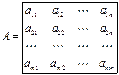
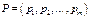 . Умножая этот вектор на столбцы матрицы, получаем выражения для среднего проигрыша игрока
. Умножая этот вектор на столбцы матрицы, получаем выражения для среднего проигрыша игрока 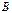 , который не превосходит цены игры
, который не превосходит цены игры 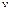 :
: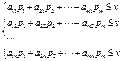
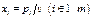 сумма которых равна
сумма которых равна 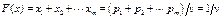 , и учитывая, что игрок
, и учитывая, что игрок 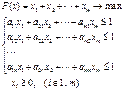
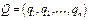 , получим (ЗЛП- II ), двойственную к (ЗЛП- I ):
, получим (ЗЛП- II ), двойственную к (ЗЛП- I ):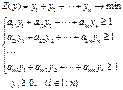
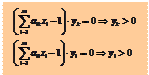
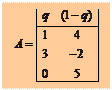
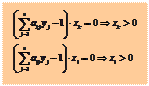 В частности при игре с матрицей
В частности при игре с матрицей 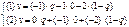
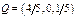 .
.
 Игра
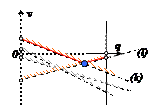
Игра 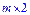 :Решается аналогично с той лишь разницей, что сначала решается задача для игрока В в которой ищется минимум верхней огибающей.
:Решается аналогично с той лишь разницей, что сначала решается задача для игрока В в которой ищется минимум верхней огибающей.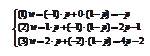 q =3/4, (1- q) =1/4
q =3/4, (1- q) =1/4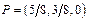
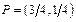 Цена игры – 7/4
Цена игры – 7/4






