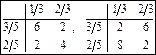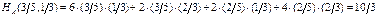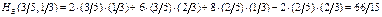БИМАТРИЧНАЯ ИГРА 2×2: ОПРЕДЕЛЕНИЕ И ВОЗМОЖНЫЕ СТРАТЕГИИ ИГРОКОВ
 и и 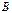 не являются противоположными не являются противоположными 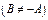 . В этом случае у каждого игрока будет своя платежная матрица. Такие игры называют биматричными. Ограничимся рассмотрением биматричных игр 2×2, когда у каждого игрока всего по две стратегии: . В этом случае у каждого игрока будет своя платежная матрица. Такие игры называют биматричными. Ограничимся рассмотрением биматричных игр 2×2, когда у каждого игрока всего по две стратегии: 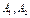 и и 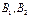 соответственно. Матрицы игры в этом случае – квадратные матрицы 2-го порядка соответственно. Матрицы игры в этом случае – квадратные матрицы 2-го порядка СРЕДНИЕ ВЫИГРЫШИ ИГРОКОВ. РАВНОВЕСНАЯ СИТУАЦИЯ
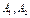 вероятности вероятности 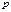 и и 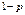 , а стратегиям , а стратегиям 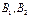 вероятности вероятности 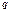 и и 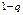 соответственно. соответственно. Средний выигрыш игрока Средний выигрыш игрока Пара чисел
То есть отклонение от оптимальной стратегии одного из игроков при условии, что другой придерживается своей оптимальной стратегии, уменьшает средний выигрыш отклонившегося игрока. ТЕОРЕМА НЕША Любая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях. НАХОЖДЕНИЕ РАВНОВЕСНЫХ СИТУАЦИЙ Введем обозначения: Пусть игрок решение которой дает Аналогично, если игрок
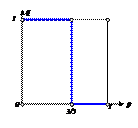
Изобразим обе полученные линии в координатах | ПРИМЕР 7.Решение и графическая иллюстрация  биматричной игры биматричной игры
Совместим оба графика. Получилась одна точка пересечения
Средний выигрыш игрока
Средний выигрыш игрока
|
Биматричные игры
|
|

Сейчас читают про:
 2015-06-28
2015-06-28 911
911

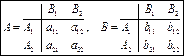
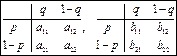
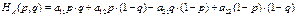 .
.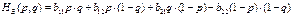
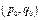 определяет равновесную ситуацию, если
определяет равновесную ситуацию, если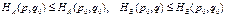 для всех
для всех 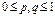 .
.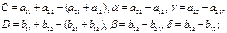 с учетом которых средние выигрыши игроков запишутся в виде:
с учетом которых средние выигрыши игроков запишутся в виде: 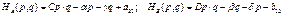 .
.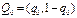 . Запишем условие равновесия для среднего выигрыша игрока
. Запишем условие равновесия для среднего выигрыша игрока 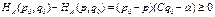 . Откуда получаем систему
. Откуда получаем систему 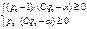 ,
,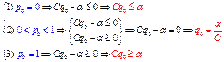
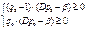
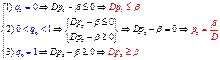
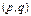 . Точки пересечения этих линий, лежащие в квадрате
. Точки пересечения этих линий, лежащие в квадрате 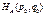 и
и 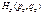 .
.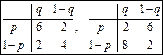
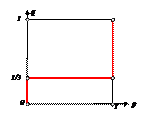 а)
а) 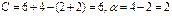 . Получим систему:
. Получим систему: 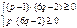 , решение которой дает
, решение которой дает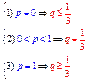
 б)
б) 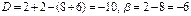 . Получим систему:
. Получим систему: 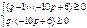 , решение которой дает
, решение которой дает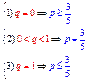
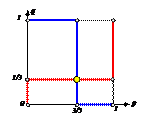
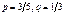 , то есть одна равновесная ситуация
, то есть одна равновесная ситуация 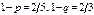 .
.