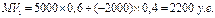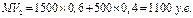ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА в общем случае представляет собой игру двух лиц, одним из которых является лицо принимающее решение, другим – природа. Лицо принимающее решение (1-й игрок) имеет  альтернативных стратегий (решений), а природа альтернативных стратегий (решений), а природа 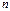 состояний, которые она принимает с заданными вероятностями. Платежная матрица состояний, которые она принимает с заданными вероятностями. Платежная матрица 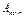 содержит прибыли (или убытки), соответствующие данному принятому решению при данном состоянии природы ( содержит прибыли (или убытки), соответствующие данному принятому решению при данном состоянии природы (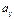 – прибыль, соответствующая – прибыль, соответствующая  -й стратегии (принятому решению) при -й стратегии (принятому решению) при 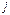 -м состоянии природы, которое она приняла с вероятностью -м состоянии природы, которое она приняла с вероятностью 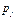 ). Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат.
Ожидаемый средний платеж для решения ). Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат.
Ожидаемый средний платеж для решения  вычисляется в виде: вычисляется в виде:
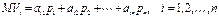 Наилучшим решением будет то, которое соответствует
Наилучшим решением будет то, которое соответствует 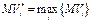 или или 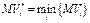 в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами). в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами).
  ФУНКЦИИ ПОЛЕЗНОСТИ. Имеются многочисленные случаи, когда при анализе ситуации с целью принятия решений в условиях риска следует использовать скорее полезность, проявляющуюсяиндивидуумами по отношению к риску, чем реальную величину платежей. ФУНКЦИИ ПОЛЕЗНОСТИ. Имеются многочисленные случаи, когда при анализе ситуации с целью принятия решений в условиях риска следует использовать скорее полезность, проявляющуюсяиндивидуумами по отношению к риску, чем реальную величину платежей.
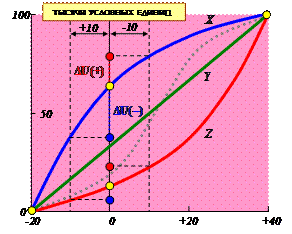
 Предположим, что имеется шанс 50 на 50, что инвестиция в 20000 у.е. или принесет прибыль в 40000 у.е., или будет полностью потеряна. Соответствующая ожидаемая прибыль: 40х0.5-20х0.5=10 тыс. у.е. Несмотря на то, что ожидается прибыль в виде чистого дохода, разные люди могут по-разному интерпретировать результат. Инвестор, склонный к риску, может сделать инвестицию, чтобы с вероятностью 50% получить прибыль в 40 тыс. у.е. Наоборот, осторожный инвестор может не выразить желания рисковать потерей 20 тыс. у.е. С этой точки зрения очевидно, что разные индивидуумы проявляю т разное отношение к риску, т.е. они проявляют разную полезность по отношению к риску. Установим произвольную шкалу полезности Предположим, что имеется шанс 50 на 50, что инвестиция в 20000 у.е. или принесет прибыль в 40000 у.е., или будет полностью потеряна. Соответствующая ожидаемая прибыль: 40х0.5-20х0.5=10 тыс. у.е. Несмотря на то, что ожидается прибыль в виде чистого дохода, разные люди могут по-разному интерпретировать результат. Инвестор, склонный к риску, может сделать инвестицию, чтобы с вероятностью 50% получить прибыль в 40 тыс. у.е. Наоборот, осторожный инвестор может не выразить желания рисковать потерей 20 тыс. у.е. С этой точки зрения очевидно, что разные индивидуумы проявляю т разное отношение к риску, т.е. они проявляют разную полезность по отношению к риску. Установим произвольную шкалу полезности 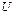 от 0 до 100 (см. рис). Если отношение лица, принимающего решение, беспристрастно к риску, то результирующая функция полезности является прямой линией, соединяющей точки (-20,0) и (40,100) (зеленая линия). В этом случае реальные деньги и их полезность
совпадают. В более реальных ситуациях функция полезности может принимать другой вид, отражающий
отношение к риску лица, принимающего решение. Так, индивидуум X осторожен, т.е. не расположен к риску (синия линия), так как проявляет большую чувствительность к потере, чем к прибыли (при изменении
в 10 тыс. у.е. вправо и влево от точки 0 у.е., увеличение прибыли изменяет полезность на величину от 0 до 100 (см. рис). Если отношение лица, принимающего решение, беспристрастно к риску, то результирующая функция полезности является прямой линией, соединяющей точки (-20,0) и (40,100) (зеленая линия). В этом случае реальные деньги и их полезность
совпадают. В более реальных ситуациях функция полезности может принимать другой вид, отражающий
отношение к риску лица, принимающего решение. Так, индивидуум X осторожен, т.е. не расположен к риску (синия линия), так как проявляет большую чувствительность к потере, чем к прибыли (при изменении
в 10 тыс. у.е. вправо и влево от точки 0 у.е., увеличение прибыли изменяет полезность на величину
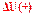 , которая меньше изменения полезности , которая меньше изменения полезности 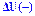 , обусловленной потерями такой же величины).
Индивидуум Z настроен на риск (красная линия). Изменения в , обусловленной потерями такой же величины).
Индивидуум Z настроен на риск (красная линия). Изменения в 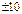 тыс. у.е. по отношению
к индивидууму Z обнаруживают противоположное поведение. Здесь тыс. у.е. по отношению
к индивидууму Z обнаруживают противоположное поведение. Здесь 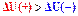 .
Индивидуум Y является нейтральным к риску (зеленая линия), так как упомянутые изменения
порождают одинаковые изменения полезности.
В общем случае индивидуум может быть как не расположен к риску, так и настроен на риск
в зависимости от суммы риска. В этом случае соответствующая кривая полезности будет иметь
точку перегиба (точечная линия).
Для определения промежуточных значений функции полезности .
Индивидуум Y является нейтральным к риску (зеленая линия), так как упомянутые изменения
порождают одинаковые изменения полезности.
В общем случае индивидуум может быть как не расположен к риску, так и настроен на риск
в зависимости от суммы риска. В этом случае соответствующая кривая полезности будет иметь
точку перегиба (точечная линия).
Для определения промежуточных значений функции полезности 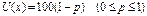 просят лицо, принимающее решение, сообщить свое предпочтение между гарантированной
наличной суммой
просят лицо, принимающее решение, сообщить свое предпочтение между гарантированной
наличной суммой 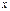 и возможностью сыграть в лотерею, в которой с вероятностью и возможностью сыграть в лотерею, в которой с вероятностью 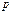 реализуется
проигрыш и с вероятностью реализуется
проигрыш и с вероятностью 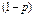 – выигрыш. Под предпочтением здесь понимают указание
нейтральной вероятности – выигрыш. Под предпочтением здесь понимают указание
нейтральной вероятности 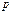 при которой с точки зрения лица, принимающего решение,
возможности сыграть в лотерею и получить гарантированную сумму при которой с точки зрения лица, принимающего решение,
возможности сыграть в лотерею и получить гарантированную сумму 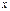 являются одинаково
привлекательными. Когда будет получено достаточное число промежуточных точек являются одинаково
привлекательными. Когда будет получено достаточное число промежуточных точек 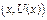 функцию полезности определяют путем регрессионного анализа или линейной интерполяцией.
функцию полезности определяют путем регрессионного анализа или линейной интерполяцией.
| ПРИМЕР
9.Вложения на фондовой бирже
Вы хотите вложить на фондовой бирже 10000 у.е. в акции одной из двух фирм 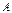 или или 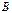 . Акции компании . Акции компании 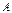 являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиций может обесцениться на 20%. Компания являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиций может обесцениться на 20%. Компания 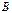 обеспечивает безопасность инвестиций с 15% в условиях повышения котировок на бирже и только 5% – в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% – понижение котировок. В какую компанию следует вложить деньги?
Информация, связанная с принятием решения, приведена в следующей таблице: обеспечивает безопасность инвестиций с 15% в условиях повышения котировок на бирже и только 5% – в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% – понижение котировок. В какую компанию следует вложить деньги?
Информация, связанная с принятием решения, приведена в следующей таблице:
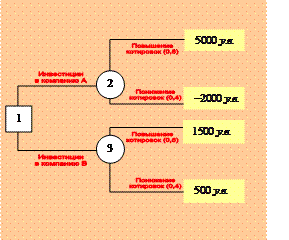
Эта задача может быть представлена в виде дерева решений. Квадратик – "решающая" вершина, а кружок – "случайная". Исходя из схемы, получаем ожидаемую прибыль за год для каждой из двух альтернатив: Для акций компании
Для акций компании
Таким образом, решением, основанным на данных вычислениях, является покупка акций компании |
Игры с природой (принятие решений в условиях риска)
|
|

Сейчас читают про:
 2015-06-28
2015-06-28 633
633