Решение систем линейных уравнений

Система m -уравнений с n неизвестными вида называется системой линейных уравнений, причем x _j – неизвестные, 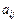- коэффициенты при неизвестных, 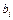- свободные коэффициенты (i=1,…,m, j=1,...n):

………………………………….

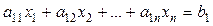
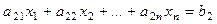
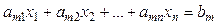
Кроме этого, система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A*x=b, где x={x_j} – вектор неизвестных, A={a_ij} – матрица коэффициентов при неизвестных при неизвестных или матрица системы, b= {b_j} – вектор свободных членов системы или векторов правых частей (i=1..m, j=1,..n).

Матрица (A|b), которая формируется путем приписывания к исходной матрице коэффициентов А столбца свободных членов b, называется расширенной матрицей системы.

Если все b_i =0, то речь идет об однородной системе линейных уравнений, иначе говорят о неоднородной системе.

Совокупность всех решений системы (x₁,x_2,…,x_n) называется множеством решений, или просто решением системы. Две системы уравнений называются эквивалентными, если они имеют одинаковое множество решений.

Однородные системы линейных уравнений Ax=0 всегда разрешимы, так как последовательность (x₁=0, x₂=0,…,x_n=0) удовлетворяет всем уравнениям системы. Решение в этом случае называется тривиальным. Проблема решения однородных систем сводится к вопросу о том существуют ли помимо тривиального другие, нетривиальные решения.

Система линейных уравнений может не иметь ни одного решения, и тогда она называется несовместной. Например в системе:

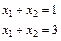
левые части уравнения совпадают, а правые различные, поэтому никакие значения x₁ и x₂ не могут удовлетворить обоим уравнения сразу.

Если же система линейных уравнений обладает решением, то она называется совместной. Совместная система называется определенной, если у нее есть единственное решение, и неопределенной, если решение больше чем одно. Так система:

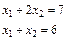
определена и имеет единственное решение 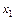=5, 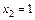, а система уравнений:

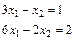
Неопределенна, так как имеет бесконечное множество решений вида 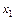= k и 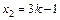, где число k произвольное.

Совокупность всех решений неопределенной системы уравнений называется общим решением, а какое-то одно конкретное решение – частным. Частное решение, полученное из общего при нулевых значениях свободных переменны, называется базисным.

При определении совместности систем уравнений важную роль играет понятие ранга матрицы. Пусть дана матрица А размером n*m Вычеркиванием из нее некоторых строк и столбцов можно получить квадратные матрицы k – го порядка, определители которых называются минорами порядка k матрицы А. Наивысший порядок не равных нулю миноров матрицы A называют рангом матрицы и обозначают r(А). Из определения вытекает, что r (A) < min(n, m), r (A) = 0, только если матрица нулевая и r (А) = п для невырожденной матрицы n -го порядка. При элементарных преобразованиях (перестановка строк матри­цы, умножение строк на число, отличное от нуля, и сложение строк) ранг матри­цы не изменяется. Итак, если речь идет об исследовании системы на совмест­ность, следует помнить, что система п линейных уравнений с т неизвестными:

> несовместна, если r (А | b) > r (А);

> совместна, если r (А | b) = г (А), причем при r(А | b) = r (А) = m имеет един­ственное решение, а при r (A | b) = r(A) < m имеет бесконечно много ре­шений.

Существует немало методов для практического нахождения решений систем линейных уравнений. Они разделяются на точные и приближенные. Метод от­носится к классу точных, если с его помощью можно найти решение в резуль­тате конечного числа арифметических и логических операций. В этом разделе на конкретных примерах будут рассмотрены только точные методы решения систем.