1.5.1. Построение двойственной задачи
Каждой задачи ЛП соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Совместное изучение данной задачи и двойственной к ней дает больше информации, чем в рассмотрении каждой из них в отдельности.
Рассмотрим задачу об использовании ресурсов: bi - запас ресурса Si; aij - число единиц i ресурса, потребляемое при производстве j продукции; cj -прибыль от одной единицы j продукции. Предположим, что некая организация решила закупить ресурсы Sj (i = 1,m) и необходимо установить оптимальные цены yi на эти ресурсы (цены ресурсов в экономической литературе называются учетными, неявными, теневыми). Покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах bi по ценам yi ,, были наименьшими.
С другой стороны, предприятия продающее ресурсы, заинтересовано в том, чтобы полученная выручка была бы не менее той суммы, которую оно может получить при переработке ресурсов в готовую продукцию. На изготовление одной единицы продукции первого вида расходуется а11 единиц S1 ресурса по цене у1 и а21 единиц ресурса S2 по цене у2 и т.д. Поэтому для удовлетворения требований продавца затраты на ресурсы при изготовлении одной единицы продукции должны быть не менее цены. В результате получим двойственную задачу:
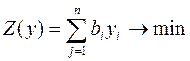 (9)
(9)
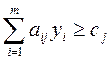 , j = 1,n (10)
, j = 1,n (10)
любой уi ≥ 0 (11)
Принцип построения двойственной задачи.
1) Если исходная задача имеет размер m×n,то двойственная задача имеет размер n×m, т.е. число переменных двойственной задачи ровно числу условий ограничений исходной задачи и наоборот (не считая условий не отрицательности переменных).
2) Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными.
3) В правых частях ограничений каждой задачи стоят коэффициенты при неизвестных в целевой функции другой задачи.
4) Если исходная задача на max и ее неравенства вида «≤», двойственная задача на min и ее неравенства «≥».
5) Каждому i ограничению:
- неравенству исходной задачи соответствует в двойственной задаче условие не отрицательности (уi ≥ 0);
- равенству соответствует переменная без ограничений и наоборот.
Пример 23. F = 3x1 + x2 - 2x4 à min
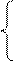 2х1 + х2 - x3 + х4 ≥ 7
2х1 + х2 - x3 + х4 ≥ 7
-х1 + 3х3 - х4 = 3
3x1 - 2х2 + х3 + 7х4 ≤ -1
х1 и х4≥0
Решение: Приведем исходную задачу к целевой установке
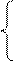 2х1 + х2 - х3 + х4 ≥ 7
2х1 + х2 - х3 + х4 ≥ 7
-х1 + 3х3 - х4 = 3
-3х1 + 2х2 - х3 - 7х4 ≥ 1
А AT
| -1 | -1 | -3 | |||||||
| -1 | -1 | ||||||||
| -3 | -1 | -7 | -1 | -1 | |||||
| -2 | min | -1 | -7 | -2 | |||||
| max |
F = 7y1 + 3y2 - y3à max
 2y1 - y2 - 3y3 ≤ 3
2y1 - y2 - 3y3 ≤ 3
y1 + 2y3 = 1
-y1 + 3y2 - y3 = 0
y1 - y2 - 7y3 ≤ -2
y1 ≥ 0, y3 ≥ 0, y2 – любое
1.5.2. Теоремы двойственности
 2015-06-28
2015-06-28 1184
1184
