Стратегические игры

Рассмотрим парную конечную игру. Пусть игрок А располагает личными стратегиями: А₁;А₂,…А_m. Аналогично игрок В: В₁,В₂,…,В_n.. Обозначим «а_i» - выигрыш игрока А, а проигрыш игрока В «-а_i». Матрица {а_ij} называется платежной матрицей.

Аi Вi	B1	B2	...	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…
--	---	---	---	---
Am	am1	am2	…	amn

Выбирая стратегию, игрок А должен помнить, что игрок В стремится «навредить» ему, а следовательно, ответит на нее такой стратегией, для которой выигрыш игрока А будет наименьшим. Нижняя цена игры (максимин) α гарантированный выигрыш игрока А при любой стратегии игрока В:

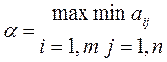. (8)

Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А. Выбирая стратегию В_j, он учитывает максимально возможный при этом выигрыш для А. Верхняя цена игры (минимакс) β – это гарантированный проигрыш игрока В:

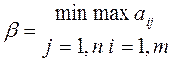. (9)

Если α = β = V, то общее значение верхней и нижней цены игры совпадает, и V называется чистой ценой игры.

Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями. Элемент a_{ij ,} являющийся одновременно и наибольшим в своем столбце и наименьшим в строке, называют седловой точкой.

8

Пример 26 Имеет ли игра седловую точку, если платежная матрица Р =

Решение.

Ai Вi	B1	B2	B3	B4	min α i
A1
A2
A3
A4
max β j					6 6

α = β = 6. Чистая цена игры V = 6. Оптимальная стратегия (А₂, В₂).

Если игра не имеет седловой точки, то применение чистых стратегией не дает оптимальное решение.

Смешанной стратегией S_А игрока А называется применение чистых стратегией А₁, А₂, …, А_m с вероятностями р₁, р₂, …, р_m, причем 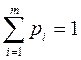. Смешанная стратегия записывается в виде:
S_A = (p₁, p₂, …, p_m). Аналогично, S_B = (q₁, q₂, …, q_n).

Оптимальное решение игры – это пара оптимальной стратегией S_A*, S_B*. Выигрыш, соответствующий оптимальному решению, называется ценой игры V.

Если чистая стратегия входит в оптимальную смешанную стратегию с не нулевой вероятностью, то она называется активной.

Теорема Неймана: каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

Теорема: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры V, если второй игрок не выходит за пределы своих активных стратегий.

Для оптимальной стратегии S_A средний выигрыш не меньше цены V, то есть:

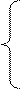а₁₁р₁ + а₂₁р₂ + … + а_m1р_m ≥ V

…

a_1np₁ + a_2np₂ + …+ a_mnp_m ≥ V

p₁ + p₂ + … + p_m = 1.

Разделим каждое уравнение на V и обозначим х_i = p_i/v, тогда

а₁₁х₁ + а₂₁х₂ + … + а_m1x_m ≥ 1

…

a_1nx₁ + a_2nx₂ + … + a_mnx_m ≥ 1

х₁ + х₂ + … + х_m = 1/V

Цель игрока А максимизировать свой гарантированный выигрыш, т.е. цену игры. Максимизация цены игры V будет эквивалентна минимизации величины 1/V. Следовательно, необходимо определить значение переменных х_i ≥ 0 так, чтобы они удовлетворяет линейным ограничениям и при этом линейная функция:

F = х₁ + х₂ + … + х_m à min.

Получим задачу ЛП, решая которую получим оптимальное решение и оптимальную стратегию S_A*:

V = 1/F_min; р_i = х_i/v

Аналогично получаем стратегию S_B:

a₁₁q₁ + a₁₂q₂ + … + a_1nq_n ≤ V

…

a_m1q₁ + a_m2q₂ + … + a_mnq_n ≤ V

q₁ + q₂ + … + q_n = 1.

Разделим каждое уравнение на V и обозначим у_j = q_j/v, тогда

a₁₁y₁ + a₁₂y₂ + … + a_1ny_n ≤ 1

….

a_m1y₁ + a_m2y₂ + … + a_mny_n ≤ 1

y₁ + y₂ + … + y_n = 1/V

Z = y₁ + y₂ + … + y_n à max

Получили взаимно-двойственные задачи.

2.3. Принятие решений в условиях неопределенности
(игры с природой)

В условиях неопределенности возникают в ситуации, когда известны все последствия всевозможных решений, но не известны их вероятности, т.е. выбор любой альтернативы может привести к одному из нескольких исходов и отсутствует даже стохастическая зависимость между альтернативами и исходами. Задачи принятия решений в условиях неопределенности моделируется игрой с природой и ее решение находится по соответствующим критериях.

Множество состояний природы обозначим через П, отдельное состояние П_j (j = 1, n). Множество решений (стратегий) статистика обозначим через А, отдельное решение – А_i (i = 1, m).

Во взаимоотношениях с природой статистик может использовать любые стратегии А₁…, А_m в зависимости от состояний П_j природы. Необходимо отыскать оптимальное решение, которое и будет его оптимальной стратегией. При этом он может пользоваться как чистыми, так и смешанными стратегиями. Пусть а_ij - эффективность комбинации (А_i, П_j), тогда получим платежную матрицу.

Матрицей риска называется матрица, элементы которой (r_ij) равны разности между максимально возможным выигрышем и тем выигрышем, которой статистик получит в тех же условиях П_j, применяя стратегию А_i, т.е.

r_ij = β_j - a_ij, где β_j = max a_ij. (10)

Оптимальную стратегию можно определить, используя ряд критериев:

а) при частичной неопределенности, если известна вероятность появления состояние П_j.

Критерий Байеса. За оптимальную стратегию принимается чистая стратегия А_i, при которой максимизируется средний выигрыш:

а* = max а_i*, где 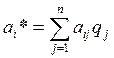(i = 1, m). (11)

или за оптимальную стратегию принимается чистая стратегия А_i, при который минимизируется средний риск, т.е

r* = min r_i*, где 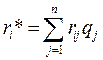(i=1, m). (12)

Критерий Лапласа. В случае, когда вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания, согласно которому все состояния природы равновероятны: q₁ = q₂ = … = q_n = 1/n.

б) при полной неопределенности.

Критерий максимакса (критерий крайнего оптимизма).Наилучшим признается решение, при котором достигается максимальный выигрыш, равный

α = max max a_ij. (13)

i j

Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствоваться принципом «или пан, или пропал».

Критерий Вальда (критерий крайнего пессимизма).

С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник типа тех, которые противодействуют в стратегических играх. За оптимальную стратегию принимает чистая стратегия, которая в наихудших условиях гарантирует наибольший выигрыш, т.е.

α = max min a_ij. (14)

i j

Критерий Сэвиджа. За оптимальную стратегию принимается стратегия, при которой величина наибольшего риска наименьша в наихудших условиях:

r = min max r_ij. (15)

i j

Критерий Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом. Согласно этому критерию, за оптимальную стратегию принимается та, при которой

max (λ min a_ij + (1 - λ) max a_ij), где 0 ≤ λ ≤ 1. (16)

j j

При отсутствии ярко выраженных склонностей целесообразно положить λ = 0.5.

Обобщенный критерий Гурвица. Предположим для определенности, что игра с природой задана матрицей выигрышей А. Переставим выигрыши a_i1, a_i2, …, a_in при каждой стратегии A_i, т.е. элементы каждой строки матрицы А, расположив их в неубывающем порядке, и обозначим получившуюся матрицу B = (b_ij). Пусть числа λ₁, λ₂, …, λ_n удовлетворяют условию λ_j ≥ 0, Σλj = 1.

Обобщенным показателем эффективности стратегии A_i назовем число G_i(λ₁, λ₂, …, λ_n) = Σλ_j*b_ij. Обобщенным критерием Гурвица относительно выигрышей с коэффициентами λ_j называется критерий, по которому оптимальной считается стратегия с максимальным показателем эффективности: A* = Arg max { G_i(λ₁, λ₂, …, λ_n).

Числа 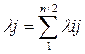и 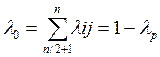назовем показателями пессимизма и оптимизма соответственно. Коэффициенты λ_j выбираются из субъективных соображений следующим образом: чем опаснее ситуация, тем ближе к единице должен быть коэффициент пессимизма; в безопасной ситуации наоборот.

Формальный способ подсчета этих коэффициентов. Пусть
b_j = Σ b_ij сумма всех выигрышей, стоящих в j -ом столбце матрицы В, 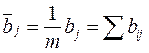среднее значение выигрышей, стоящих в j -м столбце матрицы В, 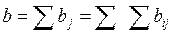сумма всех элементов матрицы В.

В случае, когда принимающий решение оценивает для себя ситуацию как опасную, он, естественно, хочет подстраховаться и потому при выборе стратегии ведет себя достаточно осторожно, проявляя больше пессимизма, чем оптимизма, поэтому показатель пессимизма должен быть больше показателя оптимизма. В этом случае показатель оптимизма можно найти по формуле: 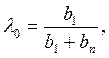а коэффициенты λ₁, λ₂, …, λ_n − в соответствии с принципом невозрастания средних выигрышей по формуле 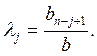Если же принимающий решение считает ситуацию безопасной, то показатель оптимизма должен быть больше показателя пессимизма. Это можно выразить выбором показателя оптимизма 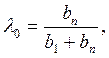и неубывающей последовательности коэффициентов λ₁, λ₂, …, λ_n по принципу неубывания средних выигрышей: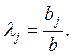

Пример 27. В соответствии со спросом на некоторую продукцию в городе планируется построить предприятия по производству этой продукции. Спрос на продукцию в течение года выражается величинами 10, 20, 30, 40 тыс. шт.

Планирующий орган предприятия может принять одно из решений: построить предприятие, которое могло бы удовлетворить спрос потребителей. Работа такого предприятия показывает, что предприятие терпит издержки в количестве 5 ден. ед. от не реализации единицы продукции, а доход от реализации составляет 15 ден. ед. Требуется:

1) придать описанной ситуации игровую схему, установить характер игры и выявить ее участников;

2) вычислить элементы платежной матрицы и составить ее;

3) дать обоснованные рекомендации планирующему органу на строительство предприятия, которое могло бы обеспечить спрос потребителей на q продукцию.

При изучении аналоговых предприятий планирующий орган располагает некоторой дополнительной информацией, снижающей неопределенность ситуации:

а) известны вероятности спроса на данную продукцию по кварталам года 0,3; 0,2; 0,4; 0,1;

б) спрос на продукцию в каждом равновероятен;

в) о вероятностях спроса на указанную продукцию по кварталам ничего определенно сказать нельзя.

Решение. В качестве статиста выступает планирующий орган, который может принять одно из следующих решений:

А₁- построить предприятие, способное удовлетворит спрос в 10 тыс. ед.; А₂ - спрос в 20 тыс. ед.; А₃ - спрос в 30 тыс.ед.; А₄ - спрос в 40 тыс.ед.

Природой выступает совокупность объективных внешних условий, в которых формулируется спрос потребителей: П₁ - спрос равен 10 тыс. ед.; П₂ – 20 тыс. ед; П₃ – 30 тыс. ед.; П₄ - 40 тыс. ед.

Рассчитаем элементы платежной матрицы:

(А₁, П₁): статист планирует построить предприятие N = 10 тыс. ед, что соответствует состоянию спроса в 10 тыс. ед. Доход:
а₁₁ = 10*15 = 150 тыс. ед.

(А_1, П₂): N = 10, P = 20 а₁₂ = 10*15 = 150.

(А₁, П₃): N = 10, P = 30 => a₁₃ = 10*15 = 150;

(А₁, П₄): N = 10, P = 40 => a₁₄ = 10*15 = 150;

(А₂, П₄): N = 20, P = 10. Т.к. спрос удовлетворяется лишь на 10 тыс. ед., то предприятие терпит убытки. Доход составит
a₂₁ = 10*15 - 10*5 = 100;

(А₂, П₂): N = 20, P = 20 => a₂₂ = 20*15 = 300;

(А₂, П₃): N = 20, P = 30 => a₂₃ = 20*15 = 300;

(А₂, П₄): N = 20, P = 40 => a₂₄ = 20*15 = 300;

(А₃, П₁): N = 30, P = 10 => a₃₁ = 10*15 - 20*5 = 50;

(А₃, П₂): N = 30, P = 20 => a₃₂ = 20*15 - 10*55 = 250;

(А₃, П₃): N = 30, P = 30 => a₃₃ = 30*15 = 450;

(А₃, П₄): N = 30, P = 40 => a₃₄ = 30*15 = 450;

(А₄, П₁): N = 40, P = 10 => a₄₁ = 10*15 - 30*5 = 0;

(А₄, П₂): N = 40, P = 20 => a₄₂ = 20*15 - 20*5 = 200;

(А₄, П₃): N = 40, P = 30 => a₄₃ = 30*15 - 10*5 = 400;

(А₄, П₄): N = 40, P = 40 => a₄₄ = 40*15 = 600.

Получим платежную матрицу.

	П1	П2	П3	П4
A1
A2
A3
A4

Вычислим средний выигрыш, используя различные критерии в условиях частичной неопределенности.

а) Критерий Байеса. Для подсчета столбца a_i в «Мастере функций» выбираем команду СУММПРОИЗ и вводим массив 1 – строка q; массив 2 – строка А_i. Оптимальная стратегия А₃.

	П1	П2	П3	П4
A1
A2
A3
A4
q	0,3	0,2	0,4	0,1	мах - 310

б) Критерий Лапласа: q₁ = q₂ = q₃ = q₄ = ¼. Оптимальная стратегия А_{3 .}

	П1	П2	П3	П4
A1
A2
A3
A4
q	0,25	0,25	0,25	0,25	мах - 325

в) Критерий Сэвиджа. Построим матрицу рисков: r_ij = β_j - a_ij, где β_j = max a_ij: r₁₁ = β₁ - a₁₁, β₁ = max a_i1 = 150 => r₁₁ = 0;

r₁₂ = β₂ - a_12, β₂ = max a_i2 = 300 => r₁₂ = 150;

r₁₃ =450 - 300; r₁₄ = 600 – 150 = 450;

r₂₁ = 150 – 100 = 50; r₂₂ = 300 – 300 = 0; r₂₃ = 450 – 300 = 150;

r₂₄ = 600 – 300 = 300; r₃₁ = 150 – 50 = 100; r₃₂ = 300 – 250 = 50;

r₃₃ = 0; r₃₄ = 600 – 450 = 150; r₄₁ = 150 – 0 = 150;

r₄₂ = 300 – 200 = 100; r₄₃ = 450 – 400 = 50; r₄₄ = 0.

Оптимальная стратегия A₃ и A_4.

					мах
R =
				мин

д) Критерий Байеса для матрицы риска. Оптимальная стратегия A₃.

					ai
R=
q	0,3	0,2	0,4	0,1	Мин - 45

е) Критерий Лапласа: q₁ = q₂ = q₃ = q₄ = ¼. Оптимальная стратегия A₃.

					ai
					237,5
R=					137,5
					62,5
					87,5
q	0,25	0,25	0,25	0,25	62,5

Вычислим средний выигрыш, используя различные критерии в условиях полной неопределенности.

а) Критерий оптимиста: α = maxmахa_ij. Оптимальная стратегия А₄.

	П1	П2	П3	П4	max
A1
A2
A3
A4
				max

б) Критерий Вальда: α = maxmin a_ij. Оптимальная стратегия А_1.

	П1	П2	П3	П4	min
A1
A2
A3
A4
				max

в) Критерий Гурвица λ = 0,5. Оптимальная стратегия А₄.

	П1	П2	П3	П4	(1 – λ)*max	λ*min	∑
A1
A2
A3
A4
						max

Ответ: принять стратегию А₃, т.е. построить предприятие мощностью 30 т.ед., прибыль при этом составит:

а) если вероятность спроса известна, то 290 т.ед.;

б) при равновероятном условии 300 т.ед.

Пример 28. Инвестор может приобрести акции одной из трех компаний. Доходность акций зависит от состояния рынка ценных бумаг. Имеются статистические данные о доходности акций за четыре месяца

A = 8 4 6 20

7 7 7 7

6 12 8 10.

Инвестору необходимо принять решение, какой из компаний отдать предпочтение.

Решение. Воспользуемся обобщенным критерием Гурвица в опасной и безопасной ситуации. Составим матрицу

B = 4 6 8 20

7 7 7 7

6 8 10 12

В опасной ситуации выбираем коэффициенты λ_j по принципу невозрастания средних выигрышей:

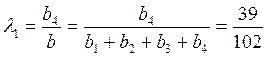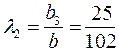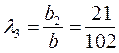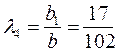; ; ; . Обобщенные показатели эффективности стратегий G ₁(λ₁, λ₂, …, λ_n) ≈ 7,98; G ₂(λ₁, λ₂, …, λ_n) = 7; G ₃(λ₁, λ₂, …, λ_n) ≈ 8,31. Оптимальной в опасной ситуации является третья стратегия.

В безопасной ситуации коэффициенты λ _j находим по принципу неубывания средних выигрышей: 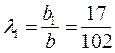; ; 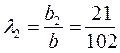; 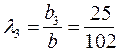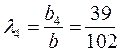. Обобщенные показатели эффективности стратегий G ₁(λ₁, λ₂, …, λ_n) ≈ 11,51; G ₂(λ₁, λ₂, …, λ_n) = 7; G ₃(λ₁, λ₂, …, λ_n) ≈ 9,69 и оптимальной в опасной ситуации является первая стратегия.

Таким образом, обобщенный критерий Гурвица различает опасную и безопасную ситуации.