Непрерывных случайных величин

Так как непрерывная случайная величина может принимать любые значения в некотором интервале, то невозможно перечислить все значения случайной величины и указать их вероятности как для дискретных величин. Для количественной характеристики распределения непрерывных случайных величин служат две основные статистические функции: функция плотности распределения вероятностей f(x) и функция распределения вероятностей (или накопленной вероятности) F(х).

Значений непрерывной величины может быть бесчисленное множество, поэтому вероятность отдельного значения равна 0. Практической мерой вероятности данного значения х служит вероятность того, что случайная величина примет значение, лежащее в каком–либо интервале Dх, например, от х=a до х+Dх=b. Плотностью распределения вероятностей называется отношение вероятности Р(a<x<b) попадания случайной величины x в тот или иной интервал Dx ее значений к величине этого интервала: . 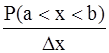Зависимость плотности распределения от значений величины x: y=f(x) называется функцией плотности распределения вероятностей (рис.3).

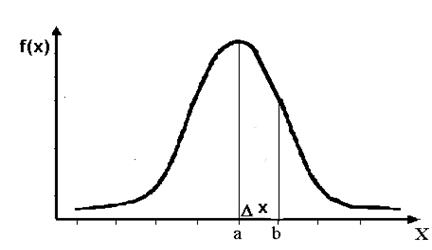Рис.3. График функции плотности распределения

вероятностей непрерывной случайной величины.

Вероятность Р(a<x<b) попадания значений случайной величины x в интервал между значениями a и b определится как площадь кривой между ординатами x=а и x=b. Эта площадь равна определенному интегралу от функции y=f(x) в этих пределах:

Р(a<x<b) = 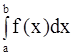= F(x) 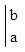=F(b) – F(a)(7)

Функция F(х) – является первообразной для у=f(х ) и называется функцией распределения вероятностей (или накопленной вероятности).

В общем случае эта функция равна вероятности того, что случайная величина Х меньше наперед заданного числа x.

F(x) = P(Х<x) (8)

При любом значении x функция распределения равно сумме вероятностей всех значений Х, меньших x. Как и всякая вероятность, функция распределения не может быть отрицательной и больше единицы 0 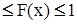(рис.4).

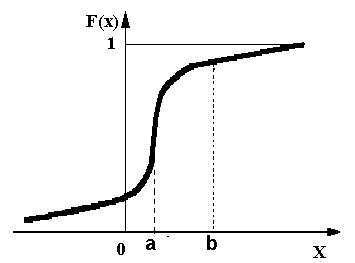Рис.4. Примерный график функции распределения

непрерывной случайной величины.

Вероятность попадания случайной величины на отрезок (а, в) равна приращению функции распределения на этом отрезке:

Р(a<x<b)=F(b) – F(a) (9)

Условие X<x можно записать в виде двойного неравенства:

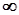- <X<x, тогда выражение (7) примет вид:

Р(- 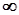<X<x)= 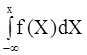= F(x) (10)

Если промежуток изменения случайной величины от - 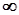до + 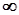, то попадание в такой интервал является достоверным событием и его вероятность равна 1.

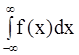= 1 (11)

Это соотношение называется условием нормировки функции плотности распределения вероятностей. Для непрерывной случайной величины с плотностью распределения y = f(x) математическое ожидание М(x) и дисперсия D(x) вычисляется по следующим формулам:

М(x)= 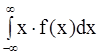, D(x)= 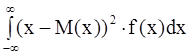(12)

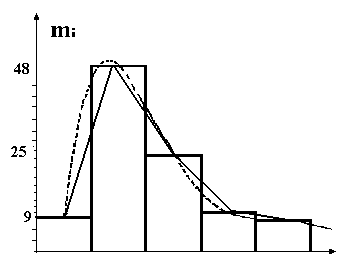
На практике выполняют построение приближенного графика функции плотности распределения вероятностей случайной величины – гистограммы. Для этого промежуток возможных значений случайной величины разделяется на ряд равных интервалов: Dx₁=x₁¸x₂; Dx₂=x₂¸x₃;...; Dx_n=x_n-1¸x_n и определяется частота (m_i) появления тех или иных значений данной величины в этих интервалах (классах). Например, изучается распределение студентов на 1 курсе по возрасту. Полученные значения распределили по 5 интервалам с Dx_i =3:

возраст по годам [15–18) [18–21) [21–24) [24–27) [27–30)

число студентов 9 48 25 10 8

Значения абсолютных или относительных частот в соответствующем масштабе откладываются на графике в виде площадей прямоугольников, построенных на отрезках Dx₁ , Dx₂ ,... Dx_n, как на основаниях.