Из формулы 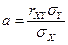 выразим
выразим 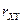 . Получим
. Получим 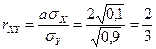 .
.
Свойства математического ожидания и дисперсии.
1. X, Y как зависимые, так и независимые случайные величины, тогда
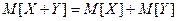 ,
,
2. 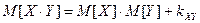 .
.
Если X, Y – некоррелированные, то 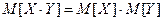 .
.
Если X, Y – независимые, то 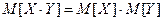 .
.
3. 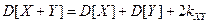
Если X, Y – некоррелированные, то 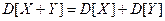 .
.
4. Если X, Y –независимые, то 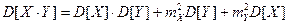 .
.
Пример 11. Даны законы распределения случайных величин X, Y:
| xi | – 1 | ||
| pi | 0,2 | 0,2 | 0,6 |
| yj | |||
| pi | 0,3 | 0,5 | 0,2 |
Найти 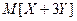 .
.
Решение.
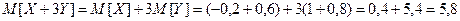 .
.
 2015-06-28
2015-06-28 429
429








