Найдем возможные значения случайного вектора (Х + У): 1 + 3 = 4, 2 + 3 =5, 1 + 5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
Р (Х = 1, У = 3) = 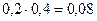 , Р (Х = 2, У = 3) =
, Р (Х = 2, У = 3) = 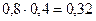 , Р (Х = 1, У = 5) =
, Р (Х = 1, У = 5) = 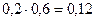 ,
,
Р (Х = 2, У = 5) = 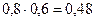 .
.
Следовательно, ряд распределения случайного вектора (Х + У) имеет вид:
| Х + У | ||||
| р | 0,08 | 0,32 | 0,12 | 0,48 |
Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 10. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
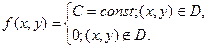
В силу свойства 2 плотности имеем, что 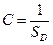 , где
, где 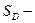 площадь области D. Тогда вероятность попадания случайной точки в некоторую область
площадь области D. Тогда вероятность попадания случайной точки в некоторую область 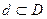 плоскости (Оxy) находится по формуле:
плоскости (Оxy) находится по формуле:
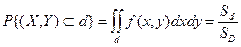 .
.
Определение 11. Пусть Х и У независимыевеличины, распределенные по нормальному закону, их плотности распределения имеет вид:
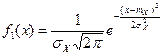 ,
, 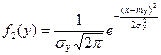 ,
,
Следовательно, плотность распределения системы (Х, У) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
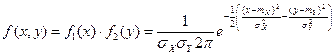 .
.
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 12. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (x, y) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты Х при условии, что Y приняла определенное значение 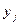 называется совокупность возможных значений
называется совокупность возможных значений 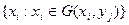 и соответствующих этим значениям условных вероятностей
и соответствующих этим значениям условных вероятностей 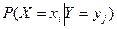 , определяемых равенством:
, определяемых равенством:
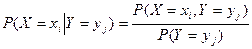 или
или 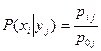 .
.
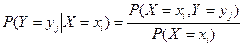 или
или 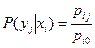 .
.
Рассмотрим СВНТ.
Условный закон распределения случайной компоненты Х при условии, что Y приняла определенное значение 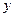 :
:
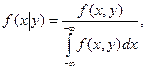
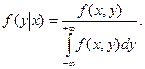
Теорема (умножения законов распределения): 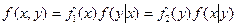 .
.
Условие нормировки: 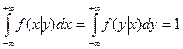 .
.
Условие независимости Х от Y: 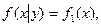 Y от Х:
Y от Х: 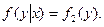
Пример 12. Случайный векторзадан таблицей распределения (См. пример № 4):
| xi \ yj | 3 | ||
| 0,2 | 0,1 | ||
| 0,3 | 0,2 | 0,2 |
Найти условные вероятности 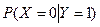 и
и 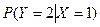 .
.
 2015-06-28
2015-06-28 558
558








