Закон больших чисел. Предельные теоремы теории вероятностей

Теория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Как и любая другая наука, теория вероятностей предназначена для того, чтобы возможно точнее предсказать результат того или иного явления или эксперимента. Если явление носит единичный характер, то теория вероятностей способна предсказать лишь вероятность исхода в весьма широких пределах. Закономерности проявляются только при большом числе случайных явлений, происходящих в однородных условиях.

Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками случайных величин и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.

Есть два типа предельных теорем: закон больших чисел и центральная предельная теорема.

Закон больших чисел, занимающий важнейшее место в теории вероятностей, является связующим звеном между теорией вероятностей как математической наукой и закономерностями случайных явлений при массовых наблюдениях над ними.

Закон играет очень важную роль в практических применениях теории вероятностей к явлениям природы и техническим процессам, связанным с массовым производством.

Предельные законы распределения составляют предмет группы теорем – количественной формы закона больших чисел. Т.е. закон больших чисел – ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным, т.е. устанавливают факт сходимости по вероятности некоторых случайных величин к постоянным. Это теоремы Бернулли, Пуассона, Ляпунова, Маркова, Чебышева.

1. а) Теорема Бернулли – закон больших чисел ( была сформулирована и доказана ранее в п. 3 § 6 при рассмотрении предельной интегральной теоремы Муавра-Лапласа.)

При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте. Иначе, вероятность того, что отклонение относительной частоты 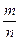наступления события А от постоянной вероятности р события А очень мало при 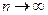стремится к 1 при любом : .

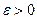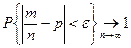b) Теорема Чебышева.

При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию иначе, если 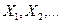независимые одинаково распределенные случайные величины с математическим ожиданием 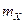и ограниченной дисперсией 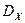, то при любом 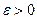справедливо: .

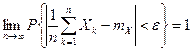Теорема Чебышева (обобщенная). Если случайные величины в последовательности 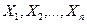попарно независимы, а их дисперсии удовлетворяют условию 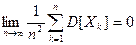, то для любого положительного ε > 0 справедливо утверждение:

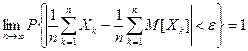или, что то же .

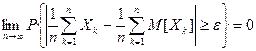c) Теорема Маркова. (закон больших чисел в общей формулировке)

Если дисперсии произвольных случайных величин в последовательности 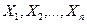удовлетворяют условию: 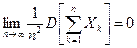, то для любого положительного ε > 0 имеет место утверждение теоремы Чебышева: .

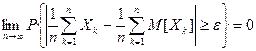d) Теорема Пуассона.

При неограниченном увеличении числа независимых опытов в переменных условиях частота события А сходится по вероятности к среднему арифметическому его вероятностей 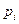при данных испытаниях.

Замечание. Ни в одной из форм закона больших чисел мы не имеем дела с законами распределения случайных величин. Вопрос, связанный с отысканием предельного закона распределения суммы 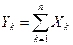, когда число слагаемых неограниченно возрастает, рассматривает центральная предельная теорема.

2. Теорема Ляпунова – центральная предельная теорема (устанавливает условия, при которых указанный предельный закон является нормальным.)

Теорема Ляпунова (простейшая форма, когда 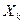взаимно независимы и одинаково распределены)

Если случайные величины 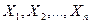взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией 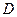, причем существует третий абсолютный момент 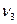, то при неограниченном увеличении 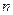закон распределения суммы неограниченно приближается к нормальному.

Замечание. Случайные величины 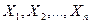, фигурирующие в теореме, могут обладать произвольными распределениями вероятностей. Если считать, что все 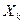одинаково распределены, то придем к интегральной теореме Муавра-Лапласа (п. 3 § 6), представляющей собой простейший частный случай центральной предельной теоремы.