Рассмотрим на одном и том же вероятностном пространстве (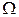 , F, P) несколько случайных величин
, F, P) несколько случайных величин 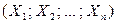 . Так как множества
. Так как множества 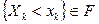 , т.е. являются событиями, то и их пересечение
, т.е. являются событиями, то и их пересечение 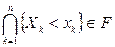 . Поэтому существует вероятность этого события.
. Поэтому существует вероятность этого события.
Определение. Многомерной функцией распределения 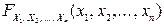 называется вероятность события
называется вероятность события 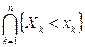 :
:
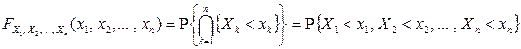 .
.
В дальнейшем изложении ограничимся случаем двух случайных величин 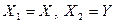 . Поэтому будем рассматривать
. Поэтому будем рассматривать 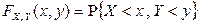 .
.
 Замечание 1. Геометрически значение
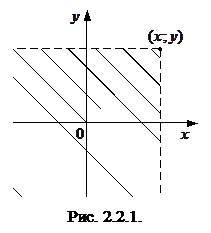
Замечание 1. Геометрически значение 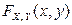 – это вероятность попадания случайной точки
– это вероятность попадания случайной точки  в бесконечный квадрант с вершиной
в бесконечный квадрант с вершиной 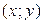 (на рис. 2.2.1 этот квадрант показан штриховкой).
(на рис. 2.2.1 этот квадрант показан штриховкой).
Замечание 2. С помощью 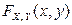 , можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:
, можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:
а) 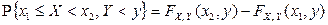 (рис. 2.2.2 а);
(рис. 2.2.2 а);
б) 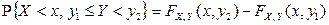 (рис. 2.2.2 б);
(рис. 2.2.2 б);
в) 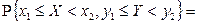
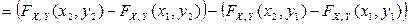 (рис. 2.2.2 в);
(рис. 2.2.2 в);
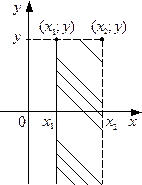
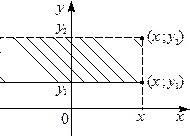
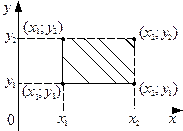
а б в
Рис. 2.2.2.
Пример 2.2.3. Дана двумерная функция распределения: 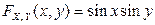 , где
, где 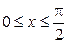 ,
, 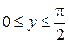 . Найти вероятность попадания случайной точки
. Найти вероятность попадания случайной точки  в прямоугольник, ограниченный прямыми
в прямоугольник, ограниченный прямыми 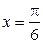 ,
, 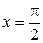 ,
, 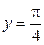 ,
, 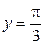 .
.
Решение. 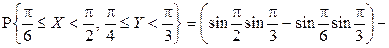
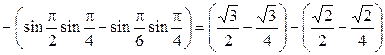
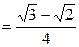 .
.
Ответ: 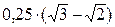 .
.
Из формулы вычисления вероятности попадания в прямоугольник и определения многомерной функции распределения 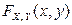 , вытекают ее свойства, которые доказываются аналогично одномерному случаю:
, вытекают ее свойства, которые доказываются аналогично одномерному случаю:
1. 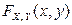 по каждому аргументу не убывает и непрерывна слева.
по каждому аргументу не убывает и непрерывна слева.
2. 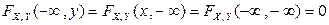 .
.
3. 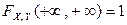 .
.
4. а) При 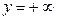 двумерная функция распределения
двумерная функция распределения 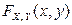 становится функцией распределения компоненты X:
становится функцией распределения компоненты X: 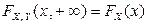 .
.
б) При 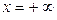 двумерная функция распределения
двумерная функция распределения 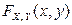 становится функцией распределения компоненты Y:
становится функцией распределения компоненты Y: 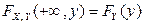 .
.
 2015-06-28
2015-06-28 1762
1762
