В двух предыдущих пунктах было показано, как, зная закон распределения системы двух (дискретных или непрерывных) случайных величин, найти законы распределения отдельных компонент X и Y.
Вопрос: «Можно ли, зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы?»
Прежде, чем ответить на этот вопрос, рассмотрим пример.
Пример 2.2.11. Законы распределений СВДТ X и Y заданы при помощи таблиц:
| X | –1 | Y | –1 | |||
| P | 0,5 | 0,5 | P | 0,5 | 0,5 |
Построим следующие две таблицы:
| Y X | –1 | 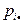 | Y X | –1 | 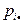 | |||
| –1 | 0,5 | 0,5 | –1 | 0,25 | 0,25 | 0,5 | ||
| 0,5 | 0,5 | 0,25 | 0,25 | 0,5 | ||||
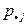 | 0,5 | 0,5 | 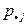 | 0,5 | 0,5 |
Распределения соответствующих компонент в одной и другой таблицах одинаковы. Однако очевидно, что эти таблицы описывают абсолютно различные распределения двумерного случайного вектора  (все значения
(все значения 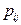 в одной таблице отличны от соответствующих значений
в одной таблице отличны от соответствующих значений 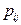 в другой таблице).
в другой таблице).
Таким образом, на поставленный выше вопрос можно дать следующий ответ: «Зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы в общем случае нельзя».
Заметим, что это можно сделать только в одном частном случае, когда случайные величины X и Y, образующие систему, независимы.
Определение. Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события.
Например, 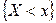 и
и 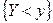 ;
; 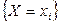 и
и 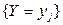 и т.д.
и т.д.
Замечание. Так как зависимость и независимость событий всегда взаимны (если событие A не зависит от события B, то и событие B не зависит от события A), поэтому зависимость и независимость случайных величин также всегда взаимны: если случайная величина X не зависит от случайной величины Y, то Y не зависит от X.
В терминах законов распределения независимость случайных величин можно определить так: «Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая».
Если компоненты X и Y двумерного вектора  независимы, то функция распределения
независимы, то функция распределения 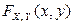 выражается, через функции распределения отдельных компонент:
выражается, через функции распределения отдельных компонент:
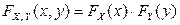 .
.
Верно и обратное утверждение. Это правило является необходимым и достаточным условием независимости для случайных величин любого типа.
Необходимые и достаточные условия независимости компонент X и Y для дискретного и непрерывного случаев:
1. X и Y являются независимыми дискретными случайными величинами тогда и только тогда, когда для всех значений индексов i и j выполняется
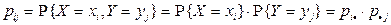 .
.
2. X и Y являются независимыми непрерывными случайными величинами тогда и только тогда, когда
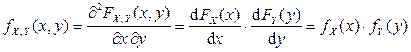 .
.
Отметим, что допускается нарушение последнего равенства на множестве точек 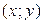 , имеющих двумерную площадь, равную нулю.
, имеющих двумерную площадь, равную нулю.
Пример 2.2.12. Закон распределения двумерного дискретного случайного вектора  задан таблицей:
задан таблицей:
| Y X | ||||
| 0,1 | 0,1 | 0,1 | 0,1 | |
| 0,05 | 0,05 | 0,05 | 0,05 | |
| 0,1 | 0,1 | 0,1 | 0,1 |
Определить, зависимы или независимы компоненты X и Y.
Решение. Составим законы распределения компонент X и Y:
| Y X | 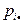 | ||||
| 0,1 | 0,1 | 0,1 | 0,1 | 0,4 | |
| 0,05 | 0,05 | 0,05 | 0,05 | 0,2 | |
| 0,1 | 0,1 | 0,1 | 0,1 | 0,4 | |
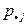 | 0,25 | 0,25 | 0,25 | 0,25 |
Проверим теперь выполнение условия 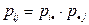 для всех пар индексов
для всех пар индексов 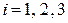 ,
, 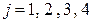 . Очевидно, что это условие выполнено для любых i и j. Значит, компоненты X и Y независимы.
. Очевидно, что это условие выполнено для любых i и j. Значит, компоненты X и Y независимы.
Ответ: компоненты X и Y независимы.
Замечание. В данном случае независимость компонент X и Y можно было установить, внимательно посмотрев на исходную таблицу, задающую закон распределения случайного вектора  . Из этой таблицы видно, что закон распределения каждой из компонент не зависит от того, какое значение приняла другая компонента.
. Из этой таблицы видно, что закон распределения каждой из компонент не зависит от того, какое значение приняла другая компонента.
Пример 2.2.13. Система двух непрерывных случайных величин  имеет плотность распределения
имеет плотность распределения
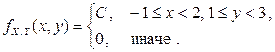
Найти константу С. Определить, зависимы или независимы X и Y. Составить функцию распределения 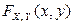 .
.
Решение. Из условия нормировки для функции плотности 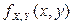 имеем:
имеем:
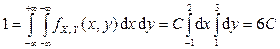 ,
,
отсюда 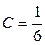 . Таким образом,
. Таким образом,
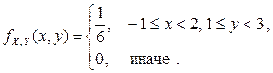
Найдем функции плотности отдельных компонент:
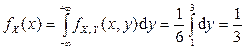 , т.е.
, т.е. 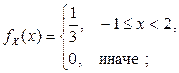
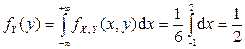 , т.е.
, т.е. 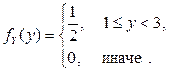
Очевидно, что равенство 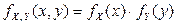 выполняется для всех точек координатной плоскости. Значит, компоненты X и Y независимы. Найдем функцию распределения системы
выполняется для всех точек координатной плоскости. Значит, компоненты X и Y независимы. Найдем функцию распределения системы 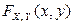 . Так как компоненты независимы, значит,
. Так как компоненты независимы, значит, 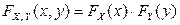 . Найдем вначале
. Найдем вначале 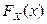 и
и 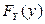 :
:
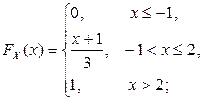

Перемножая 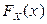 и
и 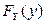 при
при 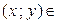 «прямоугольнику» и учитывая, что
«прямоугольнику» и учитывая, что 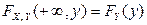 ,
, 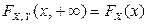 , получим:
, получим:
| Y X | 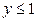 | 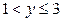 | 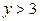 |
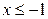 | |||
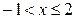 | 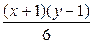 | 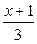 | |
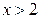 | 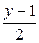 |
 2015-06-28
2015-06-28 13734
13734
