Определение. Неотрицательная кусочно-непрерывная функция 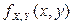 называется плотностью распределения (плотностью вероятности) двумерной случайной величины
называется плотностью распределения (плотностью вероятности) двумерной случайной величины  , если
, если
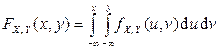 ,
,
где использована символическая запись для двойного интеграла по области 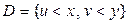 . Такая двумерная случайная величина
. Такая двумерная случайная величина  называется непрерывной.
называется непрерывной.
Функция плотности 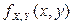 обладает следующими свойствами:
обладает следующими свойствами:
1. 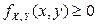 для всех
для всех 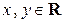 .
.
2. 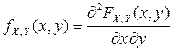 во всех точках непрерывности функции
во всех точках непрерывности функции 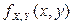 .
.
3. 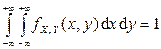 (условие нормировки).
(условие нормировки).
4. 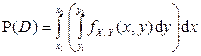 , где
, где 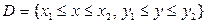 – прямоугольник на плоскости
– прямоугольник на плоскости 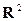 .
.
5. 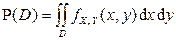 , где D – произвольная квадрируемая область на плоскости
, где D – произвольная квадрируемая область на плоскости 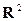 .
.
6. 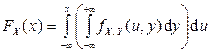 ,
, 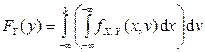 , где
, где 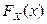 ,
, 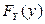 – функции распределения компонент X и Y.
– функции распределения компонент X и Y.
7. 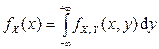 ,
, 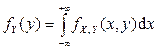 , где
, где 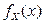 ,
, 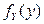 – функции плотности распределения компонент X и Y.
– функции плотности распределения компонент X и Y.
Пример 2.2.6. Известна функция плотности двумерного случайного вектора  :
:
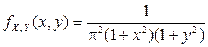 ,
, 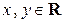 .
.
Составить функцию распределения 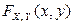 .
.
Решение. По определению функции распределения
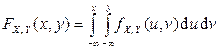 ,
,
поэтому:
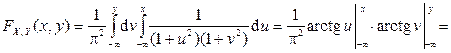
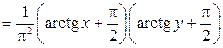 .
.
Ответ: 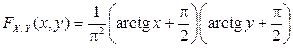 .
.
Пример 2.2.7. Найти плотность распределения двумерного случайного вектора  , если известна функция распределения
, если известна функция распределения
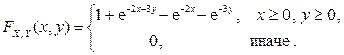
Решение. Согласно свойству 2 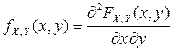 во всех точках непрерывности функции
во всех точках непрерывности функции 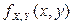 . Поэтому
. Поэтому
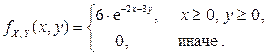
Ответ: 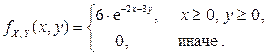
Пример 2.2.8 (двумерное равномерное распределение). Плотность 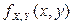 равномерного распределения на области
равномерного распределения на области 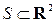 конечной двумерной площади
конечной двумерной площади 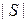 :
:
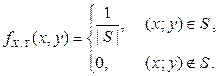
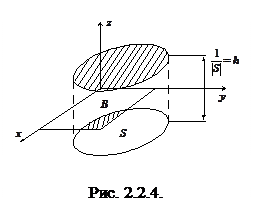 Вероятность
Вероятность 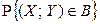 в этом случае определяется отношением площадей
в этом случае определяется отношением площадей 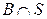 и S (рис. 2.2.4):
и S (рис. 2.2.4):
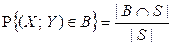 .
.
Замечание. По последней формуле вычисляются так называемые геометрические вероятности.
Пример 2.2.9. Двумерный случайный вектор  подчинен закону распределения с плотностью
подчинен закону распределения с плотностью
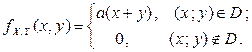
Область D – треугольник, ограниченный прямыми 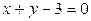 ,
, 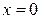 ,
, 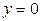 . Найти коэффициент а.
. Найти коэффициент а.
Решение. Согласно условию нормировки 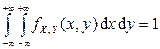 . Поскольку только в области D подынтегральная функция
. Поскольку только в области D подынтегральная функция 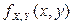 отлична от нуля, то имеем уравнение
отлична от нуля, то имеем уравнение
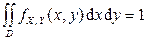 , или
, или 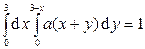 .
.
Тогда
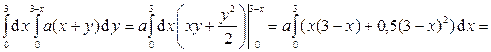
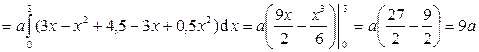 .
.
Отсюда, решая уравнение 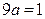 , получим
, получим 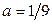 .
.
Ответ: 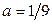 .
.
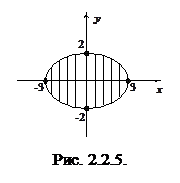 Пример 2.2.10. Известна функция плотности двумерного случайного вектора
Пример 2.2.10. Известна функция плотности двумерного случайного вектора  (рис. 2.2.5):
(рис. 2.2.5):
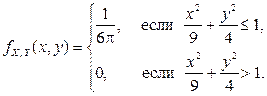
Найти плотности распределения 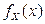 и
и 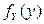 компонент X и Y.
компонент X и Y.
Решение. Очевидно, что если 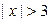 , то
, то 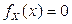 . Пусть
. Пусть 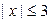 , тогда:
, тогда:
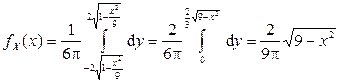 .
.
Итак, 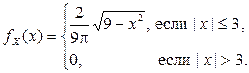
Аналогично 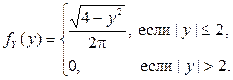
Ответ: 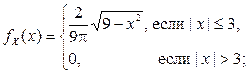
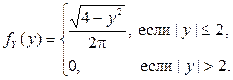
 2015-06-28
2015-06-28 2415
2415
