2.2.1. Найти вероятность того, что случайно брошенная точка с координатами  попадет на область D, определенную неравенствами
попадет на область D, определенную неравенствами 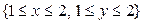 , если функция распределения координат этой точки равна
, если функция распределения координат этой точки равна
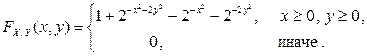
2.2.2. Пусть 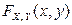 – функция распределения случайного вектора
– функция распределения случайного вектора  . Будет ли
. Будет ли 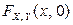 функцией распределения некоторой случайной величины? Ответ необходимо обосновать.
функцией распределения некоторой случайной величины? Ответ необходимо обосновать.
2.2.3. Является ли функция 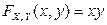 , где
, где 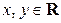 , функцией распределения некоторого случайного вектора
, функцией распределения некоторого случайного вектора  ?
?
2.2.4. Закон распределения двумерного дискретного случайного вектора  задан таблицей:
задан таблицей:
| Y X | |||
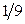 | 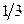 | 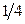 | |
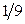 | 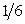 | ||
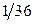 |
Найти: 1) одномерные законы распределения компонент X и Y; 2) вероятность 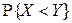 . 3) Составить функцию распределения
. 3) Составить функцию распределения 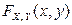 .
.
2.2.5. Закон распределения двумерного дискретного случайного вектора  задан таблицей:
задан таблицей:
| Y X | |||
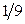 | 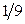 | 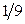 | |
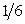 | 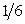 | ||
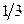 |
Найти: 1) одномерные законы распределения компонент X и Y; 2) вероятность 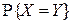 . Составить функцию распределения
. Составить функцию распределения 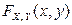 .
.
2.2.6. Монета бросается до первого выпадения герба, но не более 3 раз. Случайная величина Х – число выпадений решки, Y – число подбрасываний. Описать закон распределения случайного вектора  . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность
. Найти одномерные законы распределения компонент X и Y. Вычислить вероятность 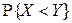 .
.
2.2.7. Стрелок 3 раза стреляет по мишени с вероятностью 0,7 попадания при каждом выстреле. Случайная величина Х – модуль разности между числом попаданий и числом промахов, Y – число попаданий. Описать закон распределения случайного вектора  . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность
. Найти одномерные законы распределения компонент X и Y. Вычислить вероятность 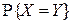 .
.
2.2.8. Система случайных величин  подчинена закону распределения с плотностью
подчинена закону распределения с плотностью
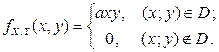
Область D – квадрат, ограниченный прямыми 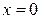 ,
, 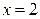 ,
, 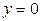 ,
, 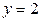 . Найти коэффициент а.
. Найти коэффициент а.
2.2.9. Случайный вектор  имеет плотность распределения
имеет плотность распределения
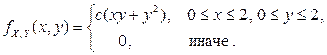
Найти: 1) постоянную c; 2) вероятность 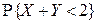 ; 3) плотности распределения компонент X и Y; 4) функции распределения компонент X и Y.
; 3) плотности распределения компонент X и Y; 4) функции распределения компонент X и Y.
2.2.10. Случайный вектор  имеет функцию распределения
имеет функцию распределения
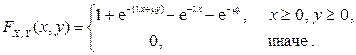
Найти законы распределения компонент X и Y.
2.2.11. Случайный вектор  имеет функцию распределения
имеет функцию распределения
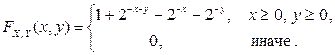
Найти: 1) двумерную плотность распределения случайного вектора  ;
;
2) вероятность попадания случайной точки с координатами  в треугольник с вершинами
в треугольник с вершинами 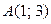 ,
, 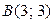 ,
, 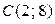 .
.
 2015-06-28
2015-06-28 1346
1346
