Метод полной математической индукции

Индукция – переход от частного к общему, дедукция – переход от общего к частному. Для конечного множества полная индукция – синоним полного перебора. Только совершив полный перебор элементов конечного множества, можно сделать общий вывод, обладают ли каким-либо свойством элементы этого множества. Принцип математической индукции позволяет осуществить в некоторых случаях полный перебор элементов бесконечного множества.

Доказательство утверждения 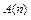методом полной математической индукции заключается в следующем:

1) Проверяется справедливость утверждения для n = 1 (база индукции).

2) Предполагается справедливость этого утверждения для 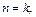где 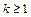(гипотеза индукции).

3) С учетом этого предположения устанавливается справедливость его для 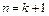(индукционный переход).

Доказательство методом неполной математической индукции некоторого утверждения, зависящего от n ³ р (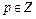), проводится следующим образом:

1) Устанавливается справедливость утверждения для n = р.

2) Предполагается справедливость утверждения для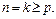

3) Исходя из этого предположения, устанавливается его справедливость для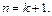

Пример. Докажите, что 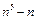делится на 30 для натурального числа n.

¨ Доказательство проведем методом полной математической индукции по числу n. При n = 1получаем, что 0 делится на 30. База индукции есть. Предположим, что при 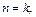утверждение верно, т.е. k ⁵ – k делится на 30. Пусть n = k+ 1. Тогда (k+ 1)⁵ – (k+ 1) = k ⁵ + 5 k ⁴ + 10 k ³ + 10 k ² + 5 k + 1 – k – 1 = (k ⁵ – k) + 5 k (k + 1)(k ² + k + 1). Первое из слагаемых делится на 30 по гипотезе индукции. Так как либо k, либо k + 1, либо k² + k + 1 делится на 3, а произведение двух последовательных целых чисел k (k + 1)делится на 2, то и второе слагаемое делится на 30. Утверждение доказано методом полной математической индукции.

Пример. Докажите, что 1³ + 2³ + 3³ + … + n ³ = n ² (n + 1)² / 4.

¨ База индукции. При n = 1 выражения, записанные слева и справа, принимают значение 1. Это значит, что база индукции есть.

Гипотеза индукции. Предположим, что при n = k, где k ³ 1, имеет место равенство

1³ + 2³ + 3³ + … + k ³ = k ² (k + 1)² / 4.

Право перехода. Пусть n = k + 1. Тогда

1³ + 2³ + 3³ + … + k ³ + (k + 1)³ = k² (k + 1)²/ 4 + (k + 1)³ =

= (k + 1)² (k ² / 4 + k + 1) = (k + 1)² (k + 2 ) ²/ 4.

Получили значение выражения слева доказываемого равенства при n = k+ 1. Утверждение доказано методом полной математической индукции.

Пример. Для каждого b > 1 и натурального n > 1 верно неравенство Бернулли bⁿ ³ 1 + n (b – 1).Докажите.

¨ n = 1; b ³ b. Верное неравенство. n = k, где k ³ 1; b^k ³ 1 +k (b – 1).

n = k + 1; b^{k+ 1} = b^k b ³ b (1 + k (b – 1)) = b + kb – k = (k + 1)(b – 1) + 1.