Множество, эквивалентное множеству 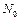 ={0, 1, 2,...}, называется счетным, и его мощность обозначается w.
={0, 1, 2,...}, называется счетным, и его мощность обозначается w.
ТЕОРЕМА. Бесконечное множеств содержит счетное подмножество.
Доказательство. Пусть  бесконечно,
бесконечно, 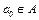 . Тогда
. Тогда  \{ a 0} тоже бесконечно. (Если предположить, что
\{ a 0} тоже бесконечно. (Если предположить, что  =
=  \{ a 0} конечно, то и
\{ a 0} конечно, то и 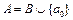 также конечно). Следовательно, существует a 1Î
также конечно). Следовательно, существует a 1Î  \{ a 0}, что
\{ a 0}, что  \{ a 0, a 1} бесконечно, и т.д. Полoжим f (0) = a 0, f (1) = a 1,... Тогда f осуществляет взаимнооднозначное соответствие между множествами
\{ a 0, a 1} бесконечно, и т.д. Полoжим f (0) = a 0, f (1) = a 1,... Тогда f осуществляет взаимнооднозначное соответствие между множествами 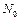 и { a 0, a 1,...}. ■
и { a 0, a 1,...}. ■
ТЕОРЕМА. Множество бесконечно тогда и только тогда, когда оно эквивалентно некоторому собственному подмножеству.
Доказательство. Пусть  бесконечно,
бесконечно,  = { b 0, b 1,...} – его счетное подмножество. Тогда
= { b 0, b 1,...} – его счетное подмножество. Тогда  = (
= ( È(
È( \
\  )) ~ (
)) ~ ( \{ b 0})È(
\{ b 0})È( \
\  ) =
) =  \{ b 0} Обратное очевидно. ■
\{ b 0} Обратное очевидно. ■
ТЕОРЕМА. Подмножество счетного множества счетно или конечно.
Доказательство. Достаточно доказать для 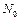 . Пусть I Ì
. Пусть I Ì 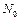 и I бесконечно. Построим f:
и I бесконечно. Построим f: 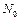 ® I. Возьмем в качестве f (0) наименьший элемент множества I, в качестве f (1) наименьший элемент множества I \{ f (0)} и т.д.; f осуществляет взаимнооднозначное соответствие между
® I. Возьмем в качестве f (0) наименьший элемент множества I, в качестве f (1) наименьший элемент множества I \{ f (0)} и т.д.; f осуществляет взаимнооднозначное соответствие между 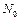 и I.
и I.
ТЕОРЕМА. Если  и
и  счетны, то
счетны, то  È
È  счетно.
счетно.
È 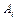 счетно, если все
счетно, если все 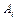 счетны.
счетны.
Доказательство. Способ нумерации элементов  È
È  :
:
1 2 ®3 4 ®... номера элементов множества  ,
,
¯ ¯
1® 2 3® 4 номера элементов множества  .
.
Способ нумерации 


 1 ® 2 3 ® 4 5 ® 6 7 …
1 ® 2 3 ® 4 5 ® 6 7 …
 | |||||
 | 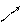 | ||||
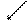 1 2 3 4 5 6 7 …
1 2 3 4 5 6 7 …


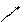


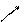 ¯
¯
1 2 3 4 5 6 7 …
ТЕОРЕМА. Если  бесконечно,
бесконечно,  – конечное или счетное множество, то (
– конечное или счетное множество, то ( È
È  )~
)~  . Если
. Если  бесконечно и несчетно,
бесконечно и несчетно,  конечно или счетно, то (А\
конечно или счетно, то (А\  )~
)~  .
.
Доказательство. Если 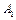 счетное подмножество множества
счетное подмножество множества  , то (
, то (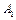 È
È  ) ~
) ~ 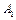 . Поэтому
. Поэтому  È
È  = (
= ( \
\ 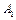 )È(
)È(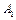 \
\  ) ~ (
) ~ ( \
\ 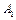 )È
)È 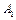 =
=  . Здесь
. Здесь  \
\  бесконечно, поэтому (
бесконечно, поэтому ( \
\  )È
)È  ~ (
~ ( \
\  ).
).
Отсюда  ~ (
~ ( \
\  ). ■
). ■
Будем говорить, что 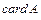 £
£ 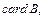 если
если  эквивалентно некоторому подмножеству множества
эквивалентно некоторому подмножеству множества  . Если
. Если 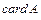 £
£ 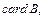 а
а  и
и  неэквивалентны, то будем писать
неэквивалентны, то будем писать 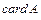 <
< 
 2015-06-28
2015-06-28 1421
1421
