Принцип включения и исключения

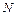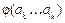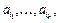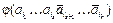ТЕОРЕМА. Пусть имеется объектов и свойства a₁,..., a_n. Обозначим через число объектов, обладающих свойствами через – число объектов, обладающих свойствами 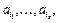но не обладающих свойствами 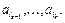Тогда число объектов, не обладающих ни одним из свойств, 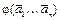определяется по формуле включения и исключения:

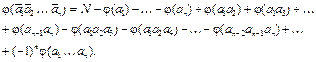(1)

Доказательство. Проведем индукцию по числу свойств. При n = l имеем

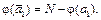(2)

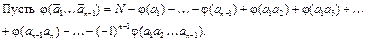(3)

Применим формулу (2) к свойству a_n:

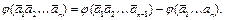(4)

Рассмотрим множество тех объектов, которые обладают свойством a_n. Среди них не обладают свойствами a ₁,..., a_{n -1}, элементы, число которых вычисляется следующим образом:

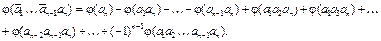(5)

Подставив в формулу (4) выражение для 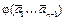из (3)
и для 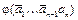из (5), получим (1).<

3адача о беспорядках. Сколько существует перестановок 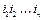чисел 1, 2,..., n таких, что 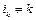для всех k = 1, 2,..., n?

Решение. Общее число перестановок 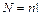Число перестановок, в которых 1 стоит на своем месте 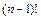, число 2 стоит на своем месте 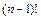... Число перестановок, в которых элементы i и j стоят на своих местах 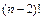Отсюда по формуле включений и исключений получаем ответ на заданный вопрос:

■

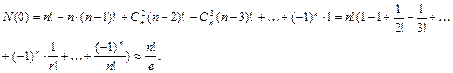Задача о встречах. Сколько существует перестановок 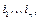в которых а_i = i точно в r местах?

■

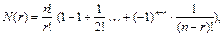Решение. так как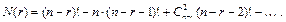

ТЕОРЕМА. Пусть 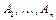– произвольные конечные множества. Тогда

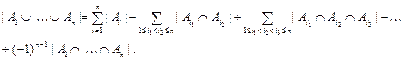
Для доказательства применить формулу включения и исключения или провести индукцию по n.