Являются ли формулы тождественно истинными:
1) 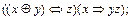
2) (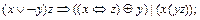
3) (x Þ y) Þ ((x Ú z) Þ y Ú z).
3.4. Алгебра Буля
Непустое множество U с тремя операциями +,  ,
, 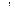 (сложение, умножение, дополнение) называется алгеброй Буля, если выполняются следующие условия:
(сложение, умножение, дополнение) называется алгеброй Буля, если выполняются следующие условия:
1) a + b = b + a, ab = ba, " a, b Î U;
2) 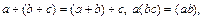 " a, b Î U;
" a, b Î U;
3) 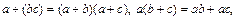 (дистрибутивность сложения относительно умножения и умножения относительно сложения);
(дистрибутивность сложения относительно умножения и умножения относительно сложения);
4) 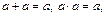 т.е. все элементы являются идемпотентами по отношения к обеим операциям;
т.е. все элементы являются идемпотентами по отношения к обеим операциям;
5) 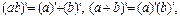 законы двойственности де Моргана;
законы двойственности де Моргана;
6) 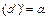
Нейтральный элемент 1 операции умножения называется универсальным элементом алгебры Буля.
Примеры.
1) 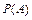 , где + = È,
, где + = È, 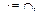
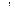 = дополнение, 0 = Æ, 1 =
= дополнение, 0 = Æ, 1 = 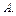
2) Алгебра высказываний, + = Ú,  = &,
= &, 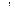 – отрицание.
– отрицание.
3) Контакты электрических сетей, если трактовать + как параллельное соединение контактов, 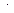 последовательное соединение контактов, 1 – есть ток в цепи, 0 – нет тока в цепи,
последовательное соединение контактов, 1 – есть ток в цепи, 0 – нет тока в цепи, 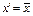 – размыкание контакта x.
– размыкание контакта x.
4) {0; 1}, a + b = max { a, b }, 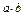 = min { a, b },
= min { a, b }, 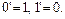
5) Множество делителей числа n, если a + b = НОК (a, b),
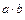 = НОД (a, b),
= НОД (a, b), 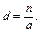
6) Сегмент [  , y ], где a + b = max { a, b },
, y ], где a + b = max { a, b }, 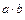 = min { a, b },
= min { a, b }, 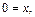
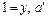 – точка, симметрическая с точкой а относительно середины сегмента.
– точка, симметрическая с точкой а относительно середины сегмента.
3.5. Эквивалентные формулы
Формулы алгебры логики  и
и  называются эквивалентными, если на всяком наборе значений переменных (входящих хотя бы в одну из формул
называются эквивалентными, если на всяком наборе значений переменных (входящих хотя бы в одну из формул  и
и  ) значения функций
) значения функций 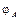 и
и 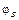 совпадают, т.е. если
совпадают, т.е. если 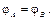 Приведем основные эквивалентности.
Приведем основные эквивалентности.
1) 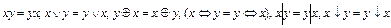 (законы коммутативности).
(законы коммутативности).
2) 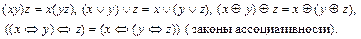
3) 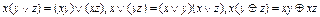 (законы дистрибутивности).
(законы дистрибутивности).
4) 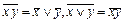 (законы двойственности де Моргана).
(законы двойственности де Моргана).
5) 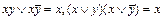 (правила склеивания).
(правила склеивания).
6) 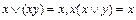 (правила поглощения).
(правила поглощения).
7) 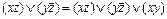 (правило обобщенного склеивания).
(правило обобщенного склеивания).
8)  &
&  =
=  ,
,  Ú
Ú  =
=  (законы идемпотентности).
(законы идемпотентности).
9) 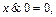
 Ú 0 =
Ú 0 = 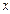 ,
,  &1 =
&1 =  ,
,  Ú 1 = 1,
Ú 1 = 1, 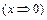 =
= 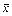 , (
, (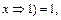 (
( Û1)=
Û1)=  ,
, 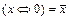 (свойства относительно констант).
(свойства относительно констант).
10) 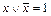 (закон исключенного третьего).
(закон исключенного третьего).
11)  &
& 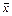 = 0 (закон противоречия).
= 0 (закон противоречия).
12) 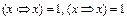 (унипотентности).
(унипотентности).
13) 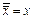 (закон двойного отрицания).
(закон двойного отрицания).
14) 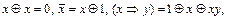
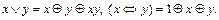
15) 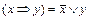 (замена импликации).
(замена импликации).
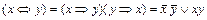 (замена эквиваленции).
(замена эквиваленции).
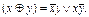
Для примера докажем свойство замены импликации: составим расчетную таблицу, в которую включаются все промежуточные вычисления.
Таблица 3.6
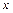 | 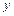 | 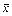 | 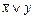 | 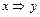 |
Столбцы значений для функций 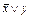 и
и 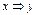 совпали, т.е. функции равны. Аналогично доказываются другие эквивалентности. Некоторые из формул можно доказывать алгебраически с помощью уже доказанных свойств. Например, для доказательства эквивалентности
совпали, т.е. функции равны. Аналогично доказываются другие эквивалентности. Некоторые из формул можно доказывать алгебраически с помощью уже доказанных свойств. Например, для доказательства эквивалентности 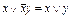 воспользуемся тем, что
воспользуемся тем, что 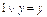 ,
, 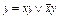 . Отсюда
. Отсюда
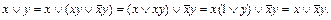
Эквивалентные формулы используются при упрощении формул. Например, упростим 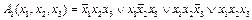 . По правилу склеивания
. По правилу склеивания 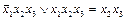 . К дизъюнкции
. К дизъюнкции 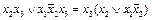 применим тождественное преобразование
применим тождественное преобразование 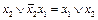 , получим
, получим 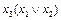 . Аналогично
. Аналогично 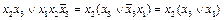 . Поэтому
. Поэтому 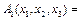
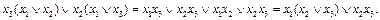
3.6. Элементарная конъюнкция. Элементарная дизъюнкция
В силу ассоциативности конъюнкции в выражениях 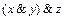 и
и
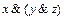 скобки можно не писать, поэтому считаем запись
скобки можно не писать, поэтому считаем запись 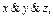 имеющей смысл. Индуктивно получает смысл запись
имеющей смысл. Индуктивно получает смысл запись 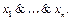 Аналогично, считаем имеющей смысл и запись
Аналогично, считаем имеющей смысл и запись 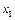 Ú
Ú 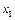 Ú…Ú
Ú…Ú 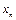 (т.е. из двуместных операций получены с помощью свойства ассоциативности n -местные). Будем полагать, что
(т.е. из двуместных операций получены с помощью свойства ассоциативности n -местные). Будем полагать, что
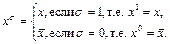
Выражение 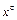 будем называть буквой, а
будем называть буквой, а 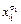 &…&
&…& 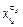 – конъюнкцией букв,
– конъюнкцией букв, 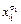 Ú…Ú
Ú…Ú 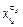 – дизъюнкцией букв.
– дизъюнкцией букв.
ТЕОРЕМА. Конъюнкция букв тождественно ложна тогда и только тогда, когда в нее входит хотя бы одна переменная вместе со своим отрицанием.
Доказательство. Þ Пусть конъюнкция букв тождественно ложна, но такой переменной в ней нет. Придадим переменным, которые входят в эту конъюнкцию, значение 1, а тем переменным, которые входят в нее под знаком отрицания, 0. На этом наборе значений переменных конъюнкция примет значение 1, а это противоречит условию, т.е. наше предположение неверно.
Ü Пусть в конъюнкцию К входит переменная t вместе со своим отрицанием. Применив закон коммутативности конъюнкции, мы приведем ее к виду 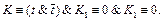 <
<
ТЕОРЕМА. Дизъюнкция букв тождественно истинна тогда и только тогда, когда существует хотя бы одна переменная, которая входит в нее вместе со своим отрицанием.
Доказывается аналогично.
Конъюнкция букв называется элементарной, если все переменные, входящие в ее различные буквы, различны. Дизъюнкция букв называется элементарной, если все переменные, входящие в ее различные буквы, различны. Количество букв, входящих в элементарную конъюнкцию (ЭК) или элементарную дизъюнкцию (ЭД), называется рангом ЭК или ЭД соответственно. Число 1 считается ЭК ранга 0. Буква считается ЭК или ЭД ранга 1. Число 0 считается ЭД ранга 0. Любую конъюнкцию букв, не являющуюся тождественно ложной, можно привести к виду элементарной, а любую дизъюнкцию букв, не являющуюся тождественно истинной, можно привести к виду элементарной также. Для этого надо применить свойства коммутативности, идемпотентности и ассоциативности конъюнкции и дизъюнкции.
 2015-06-28
2015-06-28 975
975








