2015-06-28
424
1. Докажите, что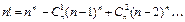 
.
2. Найдите количество чисел, не делящихся на 3, 7, 11 в первой тысяче натурального ряда.
3. Найдите сумму всех целых чисел от 1 до 1000, которые не делятся на 5 и на 7.
ГЛАВА 3. БУЛЕВЫ ФУНКЦИИ
3.1. Алгебра высказываний
Высказывание – предложение, о котором можно сказать, истинно оно или ложно. При этом оно не может быть одновременно истинным и ложным.
Отрицанием высказывания 
называется такое высказывание, которое истинно тогда и только тогда, когда ложно. Обозначается оно через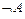 
или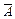 
. Читается «не ». Операция отрицания унарная. Операции, которые будут рассматриваться далее, бинарные.
Конъюнкцией двух высказываний и 
называется такое третье составное высказывание, которое истинно тогда и только тогда, когда и истинны одновременно. Для конъюнкции применяются обозначения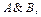 
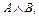
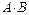(логическое умножение). Запись читается « и ».
Дизъюнкцией двух высказываний и называется такое третье составное высказывание, которое истинно тогда и только тогда, когда одно из высказываний и истинно или оба высказывания истинны одновременно. Обозначение: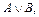 
(логическая сумма). Читается « или ».
|
|
|
Импликацией двух высказываний и называется такое третье составное высказывание, которое ложно тогда и только тогда, когда А истинно, а ложно. Обозначение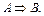 
Читается «из следует ». Здесь называют посылкой, а – следствием.
Эквиваленцией двух высказываний и называется такое третье составное высказывание, которое истинно тогда и только тогда, когда высказывания и одновременно истинны или ложны. Обозначение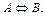 
Читается « тогда и только тогда, когда », «для необходимо и достаточно ».
Действия над высказываниями можно описать с помощью таблиц истинности. В них буква «И» соответствует значению «истина», а буква «Л» значению «ложь».
|
|
|
|
| 
|
| 
| 
| |
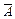
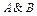
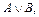
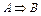
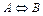
| Л | И | Л | Л | Л | Л | И | И | |
| И | Л | Л | И | Л | И | И | Л | |
| И | Л | Л | И | Л | Л | |||
| И | И | И | И | И | И |
Заметим, что двуместная операция дизъюнкции соответствует союзу «или». Но в обычной речи союз «или» употребляется, по крайней мере, в двух различных смыслах: неальтернативное неисключающее «или» и альтернативное исключающее «или». В нашем случае дизъюнкция соответствует высказыванию первого типа.
