Пусть имеется конечное множество объектов 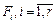 , называемых элементами (элементная база). Каждый элемент
, называемых элементами (элементная база). Каждый элемент 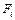 имеет
имеет 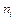 входов и один выход. Логическая сеть определяется индуктивно как объект, имеющий
входов и один выход. Логическая сеть определяется индуктивно как объект, имеющий 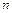 входов и p выходов.
входов и p выходов.
База индукции. Одна изолированная вершина является (тривиальной) логической сетью, причем одновременно входом и выходом (рис. 9.1).
«Индуктивный» переход основан на использовании трех операций.
1.  Объединение непересекающихся сетей. Пусть
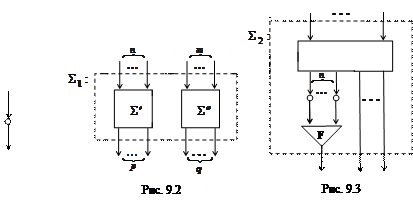
Объединение непересекающихся сетей. Пусть 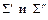 – две непересекающиеся сети, имеющие соответственно n и m входов и p и q выходов. Теоретикомножественное объединение
– две непересекающиеся сети, имеющие соответственно n и m входов и p и q выходов. Теоретикомножественное объединение  есть логическая сеть
есть логическая сеть  входами которой являются все входы
входами которой являются все входы 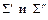 , а выходами все выходы сетей
, а выходами все выходы сетей 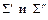 (рис. 9.2).
(рис. 9.2).
|
2. Операция присоединения элемента F. Пусть логическая сеть 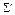 и элемент F таковы, что число n входов F не больше числа выходов
и элемент F таковы, что число n входов F не больше числа выходов 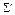 . Объявим логической сетью
. Объявим логической сетью 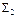 фигуру, входами которой являются входы сети
фигуру, входами которой являются входы сети 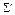 . При этом отождествим n выходов сети
. При этом отождествим n выходов сети 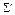 с n входами элемента F, а остальные выходы
с n входами элемента F, а остальные выходы 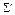 и выход элемента F объявим выходами сети
и выход элемента F объявим выходами сети 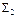 . Такая сеть называется результатом подключения элемента F к логической сети
. Такая сеть называется результатом подключения элемента F к логической сети 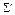 (рис. 9.3).
(рис. 9.3).
3. Операция расщепления выхода. Пусть дана логическая сеть 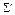 . Выделим в ней один из выходов с номером j. Объявим логической сетью фигуру, входами которой являются входы
. Выделим в ней один из выходов с номером j. Объявим логической сетью фигуру, входами которой являются входы 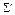 , а выходами – все выходы логической сети
, а выходами – все выходы логической сети 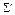 с номерами 1, 2, ¼, j – 1, j + 1, ¼ и еще два выхода, возникших из выхода с номером j сети
с номерами 1, 2, ¼, j – 1, j + 1, ¼ и еще два выхода, возникших из выхода с номером j сети 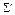 .
.
Других логических сетей нет.
Схемой из функциональных элементов называется логическая сеть 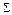 , входам и выходам которой приписаны различные буквы
, входам и выходам которой приписаны различные буквы 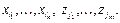 Полученную таким образом схему обозначим
Полученную таким образом схему обозначим 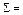
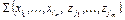
Каждый элемент 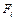 является элементарным преобразователем, который преобразует входной набор
является элементарным преобразователем, который преобразует входной набор 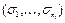 в выходные значения
в выходные значения 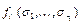 . Если на входы
. Если на входы 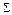
 подать набор
подать набор 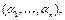 то, продвигаясь от входов к выходам, он будет переходить в набор
то, продвигаясь от входов к выходам, он будет переходить в набор 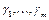 , характеризующий состояние выходов, т.е.
, характеризующий состояние выходов, т.е. 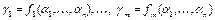 .
.  Для произвольной системы булевой функции
Для произвольной системы булевой функции 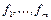 в исходной элементной базе
в исходной элементной базе 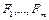 существует схема
существует схема 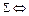 система функций
система функций 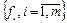 полна. В частности, в элементной базе {инвертор, конъюнктор, дизъюнктор} можно реализовать любую булеву функцию.
полна. В частности, в элементной базе {инвертор, конъюнктор, дизъюнктор} можно реализовать любую булеву функцию.
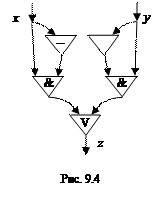 Пример. Схема из функциональных элементов рис. 9.4 реализует булеву функцию
Пример. Схема из функциональных элементов рис. 9.4 реализует булеву функцию 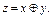
 2015-06-28
2015-06-28 800
800








