Детерминированные функции

Рассмотрим множество k -значных последовательностей 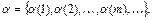где 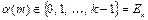для любого m = 1, 2, ¼ Рассмотрим функции, преобразующие наборы k -значных последовательностей в k -значные последовательности. Перейдем к векторной записи наборов и функций. Обозначим набор переменных 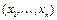через Х. Будем писать 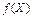вместо 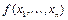. При этом значением переменной Х является набор 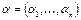, компонентами которого являются последовательности 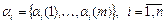, т.е. будем истолковывать 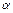как последовательность векторов 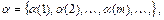где 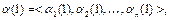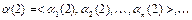можно рассматривать как числа в k -ичном исчислении, т.е.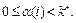

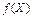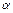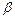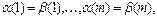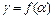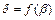Функция называется детерминированной, если для любых последовательностей и таких, что значения и функции f также совпадают в первых m координатах, т.е. 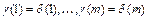. Через 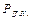обозначим множество всех детерминированных функций. Таким образом, детерминированная функция 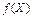определяется последовательностью функций k -значной логики:

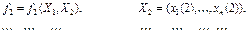
Поэтому мощность множества 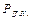всех детерминированных функций, зависящих от 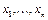, равна континууму.

Пример. Функция 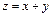, представляющая сложение двух k -значных последовательностей с бесконечным числом разрядов:

+

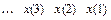
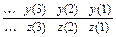
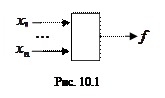
Детерминированная функция 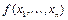может быть представлена в виде некоторого «дискретного преобразователя», в котором n входов 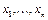и один выход 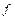. На входы в момент времени t = 1, 2, ¼ подаются входные последовательности: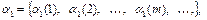

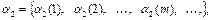
¼ ¼ ¼

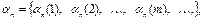и в эти же моменты t на выходе возникает выходная последовательность 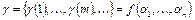. Очевидно, что в дискретном преобразователе значение 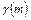зависит только от значений входных последовательностей в моменты времени t = 1, 2, ¼, m и не зависят от значений в будущие моменты времени. Поэтому преобразование 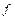– детерминированная функция. Все последовательности 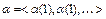рассматриваем как нульместные функции. Эти константы интерпретируются дискретным преобразователем без входов (генератором).