Резервирование как метод повышения надежности и комбинаторные схемы при анализе надежности сложных систем

Надежность сложной технической системы, в которой передача ин­формации происходит через несколько составных частей, можно опре­делить, пользуясь надежными показателями каждой части (блока).

Одной из наиболее часто встречающихся структур сложной сис­темы является последовательное соединение ее элементов. Такое со­единение работоспособно, если все части системы работоспособны. В случае взаимного влияния предшествующих блоков на работоспо­собность данного вероятность безотказной работы всей системы:

Р_сист = Р(x₁) Р(x₂/x₁)Р(x₃/x₁ x₂)... Р(х_п /x₁,..., x_n-1),

где под Р(х_i /x_i-1,..., x_i) понимается вероятность безотказной работы i -го блока при условии безотказности работы всех предшествую­щих блоков.

При статистической независимости отказов отдельных блоков системы Р_сист = Р(х₁)Р(х2)…Р(х_n), где P(x_i) - вероятность безот­казной работы i- го блока.

Такая схема работы всего устройства получила название последо­вательного соединения (с точки зрения определения надежности всей системы). Другими словами, при последовательном соединении отказ любого блока (части системы) приводит к отказу всей системы.

Другим крайним случаем при оценке работоспособности системы является случай, когда система остается работоспособной, если хотя бы один из ее блоков работоспособен. Такой случай с точки зрения характеристик надежности называют параллельным соединением блоков.

Параллельное соединение элементов соответствует так называе­мому резервированию. Резервированием называется такое соедине­ние деталей или изделий, при котором отказ наступает только после отказа основного и всех резервных изделий. На рис.7 приведены основные методы резервирования.

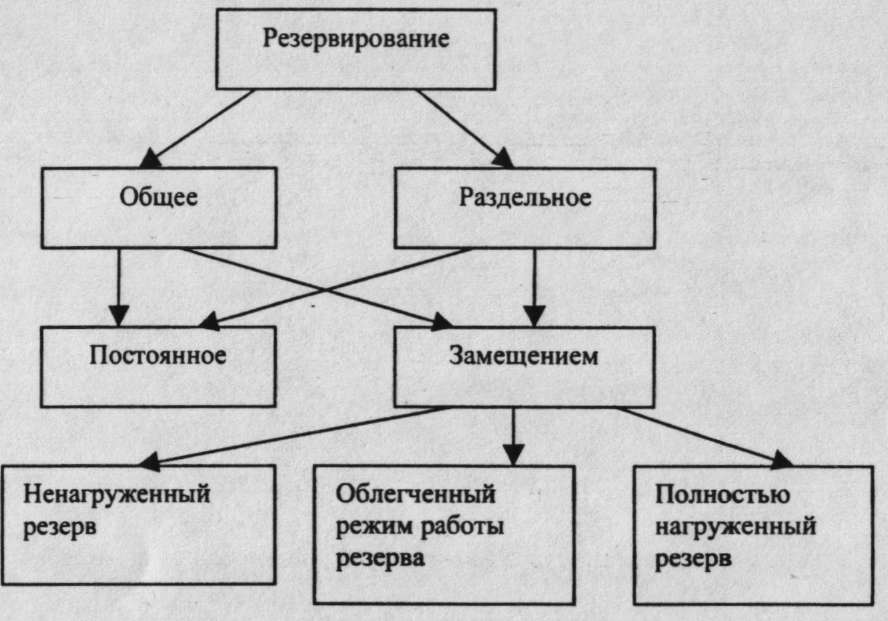
Рис.7 Основные методы резервирования

При резервировании с замещением резервные блоки могут быть постоянно включенными, или работающими в облегченном режиме, или выключенными до момента замещения. Преимущество облег­ченного режима (или выключенных резервных блоков) заключается в том, что в этих случаях интенсивность отказов резервных блоков меньше, чем у полностью нагруженного.

При расчете надежности резервированных изделий обычно дела­ют следующие предположения:

1) индикатор отказа работающего в данный момент блока и уст­ройство переключения блоков достаточно быстродействующие и безотказные;

2) резервные блоки в момент замещения находятся в работоспо­собном состоянии.

Для облегчения расчетов обычно предполагают, что интенсив­ность отказов отдельных блоков не зависит от времени, т.е. предпо­лагается экспоненциальный закон вероятности безотказной работы R(t) = e^-lt.

Количество резервируемых изделий называют кратностью ре­зервирования. Численно кратность резервирования определяется от­ношением числа резервных изделий к числу основных. Если работо­способность обеспечивается работой одного изделия, то резервиро­вание называют резервированием с целой кратностью. Если для ра­ботоспособности необходимо несколько одновременно работающих изделий (кроме наличия резервных), то такое резервирование назы­вают резервированием с дробной кратностью. Например, кратность равна 3/2, если число одновременно работающих изделий равно двум, а число резервных - трем (всего пять изделий).

При общем резервировании с постоянно включенным режимом (рис. 8, а) вероятность

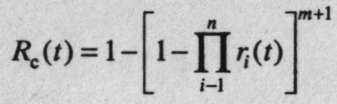безотказной работы определяется выражением

, где r_i(t) -вероятность безотказной работы i -го элемента.

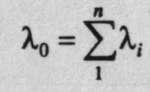
Если r(t) = e^-lt, то R(t) =1-(1- e^-l0t)^m+1, где -интенсивность отказов нерезервируемой

системы.

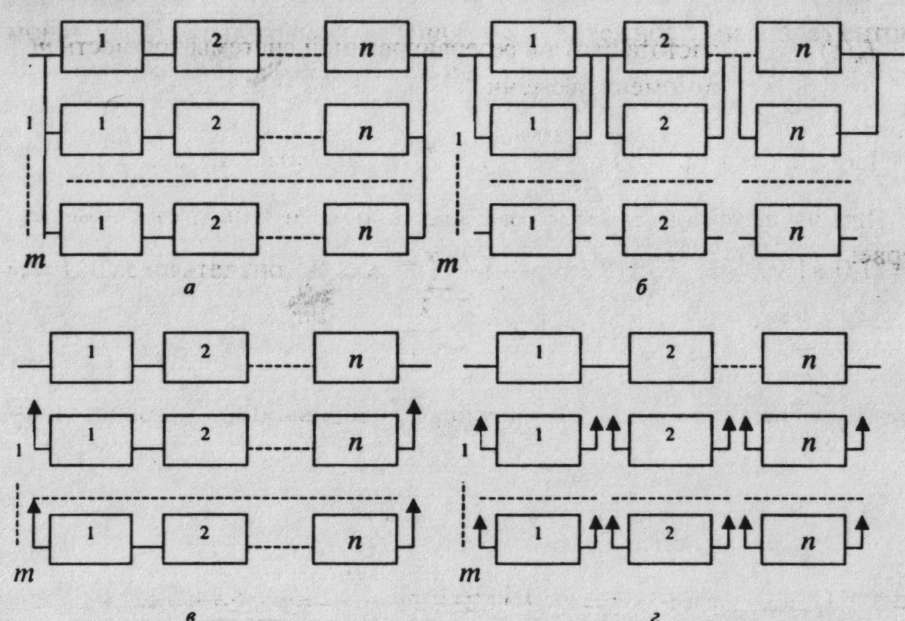Рис.8 Основные виды резервирования

При раздельном резервировании с постоянно включенным резер­вом (рис.8, б):

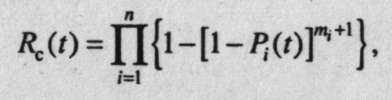где P_i(t) - вероятность безотказной работы i -гo элемента;

m_i - кратность резервирования i- гo элемента;

n - число элементов системы.

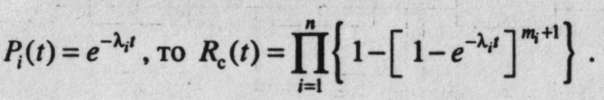
Если P_i(t) = e^-lt ,то

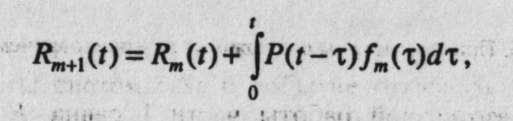При общем резервировании замещением с целой кратностью (рис.8, в):

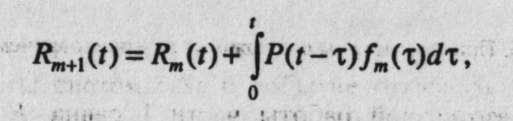где P(t -τ) - вероятность безотказной работы основной системы в течение времени (t -τ);

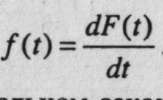f_m(τ) - частота отказов резервированной системы кратности т в момент времени τ.

Частота отказов, где F(t) – вероятность отказа.

При экспоненциальном законе надежности и ненагруженном ре­зерве:...

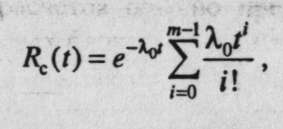где l₀ - интенсивность отказов нерезервированного устройства, а средняя наработка до первого отказа Т_ср.с = Т_ср.о(m+ 1), где - Т_ср.о - средняя наработка до первого отказа нерезервированного изделия.

При раздельном резервировании замещением с целой кратностью (рис. 8, г), величина

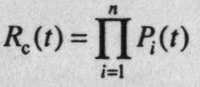вычисляется по формулам общего резервирования замещением.

На основе изученных зависимостей можно рассчитать надежность системы со сложным резервированием. В качестве примера рассмот­рим систему из 10 элементов, показанную на рис.9, и для простоты примем, что вероятность работы всех входящих в нее элементов рав­на 0,9 (кроме резервного методом замещения у которого в период ожидания, R(t) = 1). Из рис.9 видно, что система состоит из двух (I и II) неравнонадежных устройств.

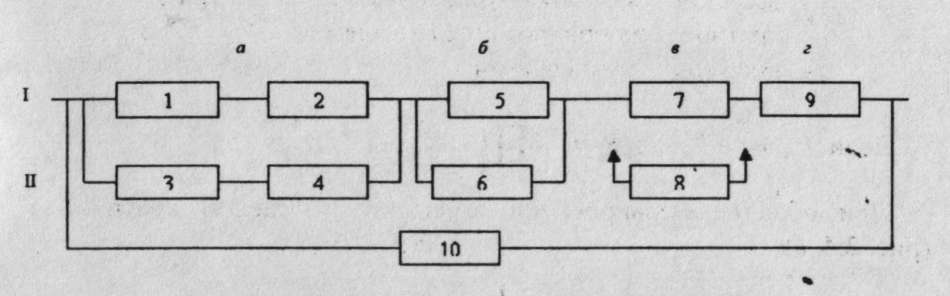
Рис. 9 Пример системы со сложным резервированием

Вероятность безотказной работы части 1 равна R₁= R_аR_бR_вR_г. Устройство I состоит из четырех узлов (а, б, в, г), причем в первых трех применяется резервирование. Часть а может быть заменена схемой параллельного включения с надежностями элементов

Р = 0,9 • 0,9 = 0,81. Тогда надежность части а равна R_a = 1 - (1 - - 0,81)² = 0,9639.

Надежность работы части б находится по такой же формуле: R_б = = 1-(1-0,9)² = 0,99.

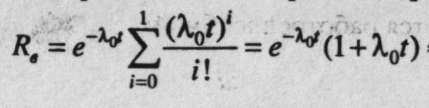Часть в в соответствии с рис.9 имеет кратность резервирования т= 1. Следовательно,

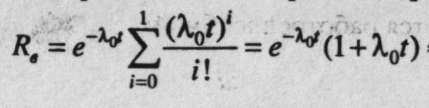= 0,9(1+0,9)= 0,99

Общая надежность устройства I будет R_i = 0,9639 • 0,99 • 0,99 = 0,85. С учетом надежности устройства II общая надежность системы: R_c = 1 - (1 - 0,85)(1 - 0,9) = 0,985.

Рассмотрим в качестве другого примера систему, показанную на рис.6, а для анализа воспользуемся методами булевой алгебры. Бло­ки A-D склонны к отказам. Любой блок может находиться в одном из двух состояний: исправном (обозначим такое состояние блока А как а) и отказавшем (обозначим как а). Очевидно, что Р(а) + Р(־а) = 1. Ос­тальные блоки описываются также (б и ˉ б, с и ˉс и т.д.), а отказы блоков предполагаем статистически независимыми. Пока существует хотя бы один путь от точки Н к точке К, система функционирует нор­мально. Обозначим это событие через S_N, и вероятность этого Р_N. ­

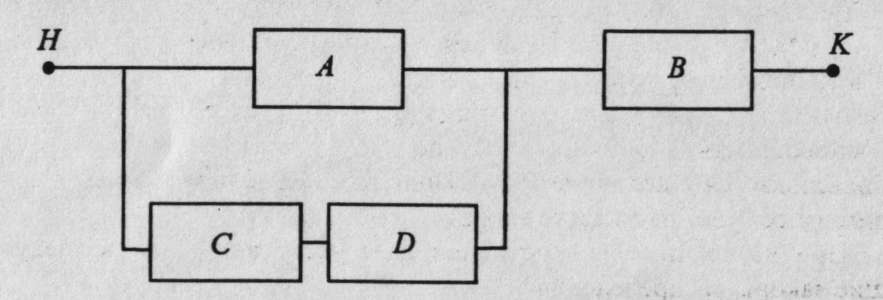Рис. 10 Иллюстрация системы с использованием методов булевой алгебры

Существует несколько методов определения Р_N. Событие нор­мальной работы системы S_N и событие отказа S_E можно выразить следующим образом с помощью булевой функции: S_N =ab + cdb = b(a + cd) и S_E =b +ˉас + ˉaˉd =ˉb + ˉa(ˉc + ˉd). Последнее выражение можно получить из предыдущего заменой перемен­ных на их отрицание, знаков логического умножение - на сложение, а сложения - на умножение (правомерность этого вытекает из тож­деств де Моргана).

Аналогичные результаты можно получить, используя метод пере­бора состояний всех блоков и определения, при каких состояниях система остается работоспособной:

S₀ = abсd S_l = abсˉd S₂ = abˉсd S₃ = abˉсˉd

S₄ = aˉbсd S₅ = aˉbсˉd S₆ = aˉbˉсd S₇ = aˉbˉсˉd

S₈= ˉabсd S₉ = ˉabсˉd S₁₀ = ˉabˉсd S₁₁= ˉabˉсˉd

S₁₂=ˉаˉbcd S₁₃= ˉaˉbсˉd S_u=ˉaˉbˉcd S_l5=ˉaˉbˉсˉd

Очевидно, что

S_N = S₀ + S₁+ S₂ + S₃ + S₄ = abсd+ abсˉd+ abˉсd +abˉсˉd+ aˉbсd = ab(cd + cˉd +ˉcd + ˉcˉd) + bcd(a + ˉa) = ab + bcd = b(a + cd), что и было получено ранее. Если возвратиться к вероятностям, то получим

P(S_N) = P(b)[P(a)+P(c)P(d)].

Численные значения P(S_N) можно получить также, используя ме­тод статистического моделирования. В каждый момент времени ме­тодом Монте-Карло определяется работоспособность каждого блока и в зависимости от этого определяется работоспособность всей сис­темы. Отношение числа испытаний, при которых сохраняется рабо­тоспособность, к общему числу испытаний при большом их числе приближается к величине P(S_N). Подробнее об имитационных экспе­риментах будет рассказано ниже.

При изучении надежности наиболее часто встречаются следую­щие законы распределения:

1. Экспоненциальный, для которого l(t) = l = const, R(t) = ехр(-lt), T_ср = 1/l. Экспоненциальное распределение широко используется благодаря его простоте и наличию прямой связи с теорией пуассоновских случайных процессов. Напомним, что для таких процессов возникновение событий в будущем не зависит от их возникновения в прошлом и исключается возможность возникновения нескольких со­бытий одновременно.

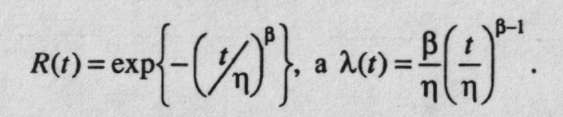
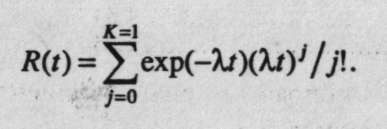2. Гамма-распределение, которое может встречаться на практике, когда отказ вызывается точно К «ударами» (отказами), каждый из которых возникает с параметром l (при К= 1 гамма-распределение сводится к экспоненциальному). Для гамма-распределения при по­ложительном целом К:

3. Распределение Вейбулла:

Такое распределение встречается, когда отказ вызван тем, что на­грузка превышает прочность в наиболее слабом месте изделия. При b=1 распределение Вейбулла переходит в экспоненциальное.

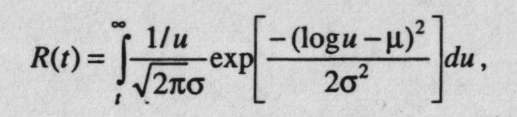4. Логарифмически нормальное распределение

где µ>0, σ>0.

В теории надежности это распределение можно получить исходя из физики процесса возникновения отказов из-за усталостных изломов.