1. Даны точки А (2; 2), В (-2; 0), С (0; 2). Найдите такую точку D (x; y), чтобы 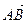 и
и 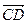 были равны.
были равны.
2. Дан ромб ABCD со стороной 1 и углом А,равным 60°. Чему равна длина суммы векторов:
1) 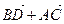 ; 2)
; 2) 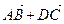 ; 3)
; 3) 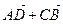 ; 4)
; 4) 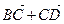 ?
?
3. В треугольнике АВС вектор 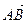 =
= 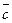 и вектор
и вектор 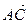 =
= 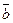 . Постройте каждый из следующих векторов:
. Постройте каждый из следующих векторов:
а) 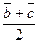 ; б)
; б) 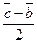 ; в)
; в) 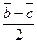 ; г) –
; г) – 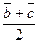 .
.
4. Докажите, что если 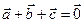 и векторы
и векторы 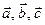 ненулевые и не коллинеарные, то из них можно составить треугольник.
ненулевые и не коллинеарные, то из них можно составить треугольник.
5. В параллелограмме ABCD точка К – середина стороны ВС, М – середина стороны CD. АВ = 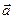 , AD =
, AD = 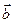 . Разложите по векторам
. Разложите по векторам 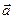 и
и 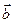 следующие векторы: 1)
следующие векторы: 1) 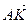 ; 2)
; 2) 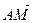 ; 3)
; 3) 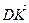 ; 4)
; 4) 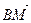 ;
;
5) 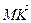 .
.
6. При каком значении k векторы 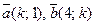 : а) коллинеарны; б) одинаково направлены?
: а) коллинеарны; б) одинаково направлены?
7. Доказать, что если для ненулевых векторов 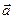 ,
, 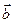 ,
, 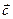 выполняются равенства:
выполняются равенства: 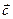 =
= 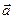 +
+ 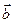 , |
, | 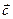 | = |
| = | 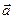 |+|
|+| 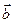 |, то векторы
|, то векторы 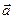 ,
, 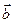 ,
, 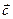 коллинеарны.
коллинеарны.
8. Доказать, что если 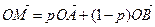 , то точки М, В, А лежат на одной прямой.
, то точки М, В, А лежат на одной прямой.
9. Найдите единичный вектор, коллинеарный вектору 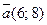 и одинаково направленный с ним.
и одинаково направленный с ним.
10. В трапеции 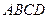 отношение оснований
отношение оснований 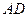 и
и 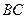 равно 3:2, диагонали трапеции пересекаются в точке F. Выразить вектор
равно 3:2, диагонали трапеции пересекаются в точке F. Выразить вектор 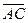 через векторы
через векторы 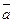 =
= 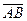 и
и 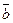 =
= 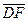 .
.
11. В треугольнике 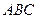 точка
точка 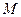 на стороне
на стороне 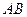 и точка
и точка 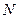 на стороне
на стороне 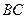 выбраны так, что |
выбраны так, что | 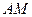 |:|
|:| 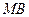 |= 2: 1, |
|= 2: 1, | 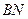 |:|
|:| 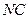 = 2: 1. Отрезки
= 2: 1. Отрезки 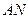 и
и 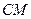 пересекаются в точке P. Найти
пересекаются в точке P. Найти 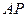 :
: 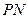 .
.
12. Точки R и Q – проекции точки Р, лежащей на стороне АВ равностороннего треугольника ABC, на его стороны АС и ВС. Доказать, что прямая, содержащая медиану РМ треугольника RQP,проходит через центр О треугольника ABC.
13. В параллелограмме ABCD 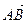 =
= 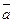 ,
, 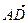 =
= 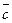 . Выразите векторы
. Выразите векторы 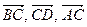 ,
, 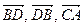 через
через 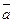 и
и 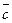 .
.
14. В треугольнике ABC точка М принадлежит стороне АВ,при этом АМ: MB = 2: 1, точки Q, N – на стороне ВС, BQ: QC = 1: 6, BN: NC = 3:2, Р – на стороне АС, АР: PC = 2: 3. Отрезки MN и QP пересекаются в точке О. Найдите МО: ON, РО: OQ.
15. 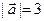 ,
, 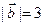 ,
, 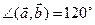 ,
, 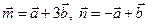 . Найдите косинус угла между векторами m и n.
. Найдите косинус угла между векторами m и n.
16. Докажите, что высоты треугольника пересекаются в одной точке.
17. В правильном треугольнике ABC со стороной равной 1, отрезок с концами Р и М на сторонах АВ и ВС пересекает отрезок ВК,точка К лежит на стороне АС. Найдите угол между прямыми ВК и РМ,если ВР: РА = 1: 2, ВМ: МС = 3: 1, АК: КС = 1: 2.
18. Докажите, что четырехугольник ABCD с вершинами А (1; 0), В (3; 3), С (-1; 2), D (3; 8) – трапеция.
19. Докажите, что для любых а, b, с, d имеет место неравенство
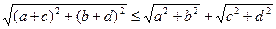 .
.
20. При каком значении х векторы 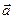 и
и 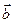 коллинеарны, если
коллинеарны, если 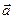 (3- х; 4),
(3- х; 4), 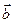 (2; 4 +х).
(2; 4 +х).
21. Решите неравенство: 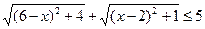 .
.
22. Даны три вектора 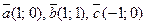 . Найдите такие числа λ и μ, чтобы выполнялось векторное равенство
. Найдите такие числа λ и μ, чтобы выполнялось векторное равенство 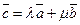 .
.
23. Даны векторы 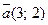 и
и 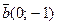 . Найдите абсолютную величину вектора -2
. Найдите абсолютную величину вектора -2 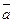 + 4
+ 4 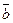 .
.
24. Найти угол между векторами 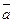 и
и 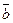 , если |
, если | 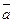 |=4, |2
|=4, |2 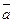 - 5
- 5 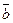 |=17, (3
|=17, (3 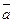 + 2
+ 2 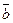 ) = 42.
) = 42.
25. Найдите длину диагонали АС ромба ABCD, у которого длины сторон равны 1 и угол BAD равен 300.
 2015-06-28
2015-06-28 1025
1025