1. Даны точки А (2; 2), В (-2; 0), С (0; 2). Найдите такую точку D (x; y), чтобы 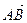 и
и 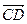 были равны.
были равны.
Решение: (на заметку, здесь и далее рассматриваются векторы, но стрелку сверху я опустила для скорости набора).
1) Найдем координаты вектора АВ: АВ(-2-2; 0-2)=АВ(-4; -2). 2) CD(x-0;y-2). 3) Приравниваем координаты: х=-4, у-2=-2, х=-4, у=0. Ответ: D(-4;0).
2. Дан ромб ABCD со стороной 1 и углом А,равным 60°. Чему равна длина суммы векторов: 1) 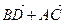 ; 2)
; 2) 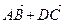 ; 3)
; 3) 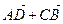 ;4)
;4) 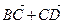 ?
?
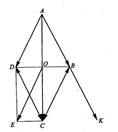 Решение: 1) т.к диагонали ромба точкой пересечения делятся пополам, то BD=2OD, AC=2OC, BD+AC=2OD+2OC=2(OD+OC). По правилу параллелограмма OD + ОС = OE. Так
Решение: 1) т.к диагонали ромба точкой пересечения делятся пополам, то BD=2OD, AC=2OC, BD+AC=2OD+2OC=2(OD+OC). По правилу параллелограмма OD + ОС = OE. Так
как ОЕ=ВС, то |OE|=1? 2|OE|=2;
2) AB + DC = АВ + BK= AK, |AK | = 2;
3) AD+CB=AD+DA=AA=O, |O|=0;
4) BC+CD=BD (по правилу треугольника). Так как 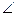 A = 60°, то ∆ABD – правильный, значит, |BD|=1.
A = 60°, то ∆ABD – правильный, значит, |BD|=1.
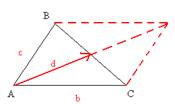
3. В треугольнике АВС вектор 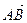 =
= 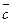 и вектор
и вектор 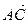 =
=  . Постройте каждый из следующих векторов: а)
. Постройте каждый из следующих векторов: а) 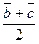 ; б)
; б) 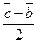 ; в)
; в) 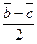 ; г) –
; г) – 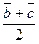 .
.
Решение: а) d- медиана из 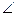 А, б) d=1/2BC; в) d=1/2BC, заметим, что длины векторов ВО и СО равны, а направление противоположно; г) d- медиана из
А, б) d=1/2BC; в) d=1/2BC, заметим, что длины векторов ВО и СО равны, а направление противоположно; г) d- медиана из 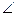 А, заметим, что длины векторов АО и ОА равны, а направления противоположны.
А, заметим, что длины векторов АО и ОА равны, а направления противоположны.
 а) а) | 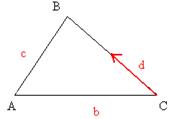 б) б) | 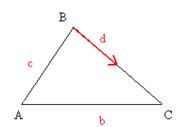 в) в) | 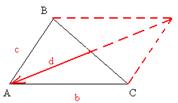 г) г) |
4. Докажите, что если 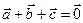 и векторы
и векторы 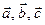 ненулевые и не коллинеарные, то из них можно составить треугольник.
ненулевые и не коллинеарные, то из них можно составить треугольник.
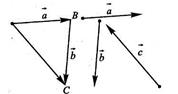 Решение: Отложим от произвольной точки А вектор АВ = а, от точки В отложим вектор ВС =
Решение: Отложим от произвольной точки А вектор АВ = а, от точки В отложим вектор ВС =  . Тогда по правилу треугольника для сложения векторов вектор АС = АВ + ВС = а + b=-- с,значит, вектор СА = - АС = с. Таким образом, треугольник А ВС составлен из векторов а = АВ, b = ВС и с = СА, что и требовалось доказать.
. Тогда по правилу треугольника для сложения векторов вектор АС = АВ + ВС = а + b=-- с,значит, вектор СА = - АС = с. Таким образом, треугольник А ВС составлен из векторов а = АВ, b = ВС и с = СА, что и требовалось доказать.
5. В параллелограмме ABCD точка К – середина стороны ВС, М – середина стороны CD. АВ= 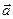 , AD=
, AD= 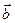 . Разложите по векторам
. Разложите по векторам 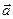 и
и 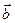 следующие векторы: 1)
следующие векторы: 1) 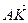 ; 2)
; 2) 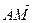 ; 3)
; 3) 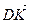 ; 4)
; 4) 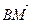 ; 5)
; 5) 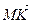 .
.
Решение: 1. По правилу треугольника АК=АВ+ВК, ВК= 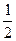 ВС=
ВС= 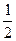
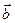 ,тогда АК =
,тогда АК = 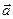 +
+ 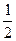
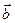 .
.
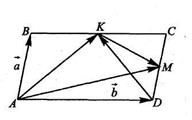 2. Аналогично пункту 1 данной задачи: AM =
2. Аналогично пункту 1 данной задачи: AM = 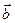 +
+ 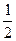
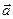 .
.
3. DK = DC + CK = 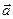 +
+ 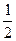 CB=
CB= 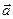 -
- 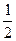 BС =
BС = 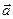 -
- 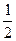
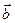 .
.
4. Аналогично пункту 2 данной задачи: ВМ = 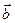 -
- 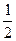
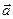 .
.
5. МК =МС + СК = 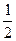 DC +
DC + 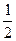 СВ =
СВ = 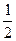
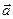 -
- 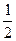
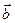 .
.
6. При каком значении k векторы 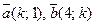 : а) коллинеарны; б) одинаково направлены?
: а) коллинеарны; б) одинаково направлены?
Решение: Из условия коллинеарности, имеем: 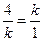 . Отсюда k2=4, k=-2, k=2 (2>0). Если k=±2 – коллинеарны, если k=2 – одинаково направлены.
. Отсюда k2=4, k=-2, k=2 (2>0). Если k=±2 – коллинеарны, если k=2 – одинаково направлены.
7. Доказать, что если для ненулевых векторов 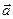 ,
, 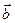 ,
, 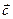 выполняются равенства:
выполняются равенства: 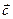 =
= 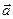 +
+ 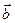 , |
, | 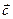 | = |
| = | 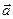 |+|
|+| 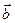 |, то векторы
|, то векторы 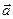 ,
, 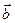 ,
, 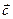 коллинеарны.
коллинеарны.
Док-во: Предположим, что векторы a, b, с неколлинеарны. Тогда из условия с = а + b следует, что векторы a, b, с образуют треугольник. Но для длин сторон треугольника, а значит, для длин векторов a, b, с выполняется неравенство: | с| < | а | + | b |. Получили противоречие с условием. Значит, векторы а, b, с коллинеарны.
8. Доказать, что если 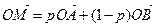 , то точки М, В, А лежат на одной прямой.
, то точки М, В, А лежат на одной прямой.
Решение: Из условия 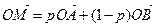 последовательно получим:
последовательно получим: 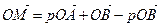 ; ОМ-ОВ=р(ОА-ОВ), ВМ=рВА. Если р≠0, то векторы ВМ и ВА коллинеарны, а точки В, М, К лежат на одной прямой; если р=0, то вектор ВМ =0 и точки В, М, А также лежат на одной прямой.
; ОМ-ОВ=р(ОА-ОВ), ВМ=рВА. Если р≠0, то векторы ВМ и ВА коллинеарны, а точки В, М, К лежат на одной прямой; если р=0, то вектор ВМ =0 и точки В, М, А также лежат на одной прямой.
9. Найдите единичный вектор, коллинеарный вектору 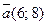 и одинаково направленный с ним.
и одинаково направленный с ним.
Решение: Найти b(x,y), |b|=1, коллинеарный вектору а(6, 8). Имеем |b|= 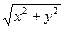 =1,
=1, 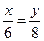 . Отсюда решая систему находим b(
. Отсюда решая систему находим b(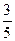 ;
; 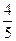 ).
).
10. 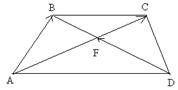 В трапеции
В трапеции 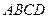 отношение оснований
отношение оснований 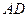 и
и 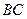 равно 3:2, диагонали трапеции пересекаются в точке F. Выразить вектор
равно 3:2, диагонали трапеции пересекаются в точке F. Выразить вектор 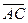 через векторы
через векторы  =
= 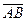 и
и  =
= 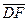 .
.
Решение. 1) Треугольники 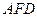 и
и 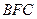 подобны по двум углам. Из подобия следует, что |
подобны по двум углам. Из подобия следует, что | 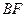 |:|
|:| 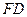 |= 2:3, откуда |
|= 2:3, откуда | 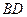 |:|
|:| 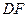 |= 5: 3.
|= 5: 3.
Следовательно, 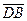 =
= 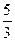
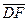 ,
, 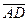 = AB+BD =a+
= AB+BD =a+ 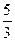
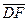 =a+
=a+ 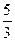 b.
b. 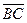 =
= 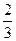 AD=
AD= 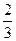
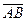 +
+ 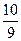
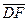 ,
, 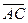 =
= 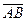 +
+ 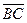 =
= 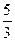
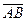 +
+ 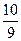
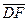 или
или 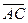 =
= 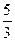
 +
+ 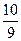
 .
.
11. В треугольнике 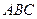 точка
точка 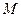 на стороне
на стороне 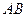 и точка
и точка 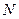 на стороне
на стороне 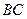 выбраны так, что |
выбраны так, что | 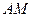 |:|
|:| 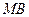 |= 2: 1, |
|= 2: 1, | 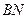 |:|
|:| 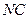 = 2: 1. Отрезки
= 2: 1. Отрезки 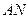 и
и 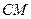 пересекаются в точке P. Найти
пересекаются в точке P. Найти 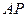 :
: 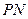 .
.
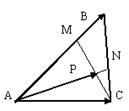 Решение. Обозначим
Решение. Обозначим 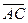 =
=  ,
, 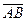 =
=  . Из условия следует, что точка
. Из условия следует, что точка 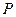 общая для двух отрезков. Поэтому выразим вектор
общая для двух отрезков. Поэтому выразим вектор 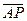 двумя способами.
двумя способами.
1) 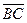 =
= 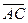 -
- 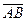 =
=  -
-  ,
, 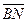 =
= 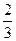
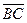 =
= 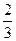
 -
- 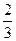
 ,
, 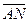 =
= 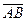 +
+ 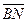 =
=
=  + (
+ (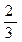
 -
- 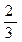
 ) =
) = 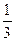
 +
+ 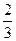
 ,
, 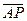 =
= 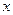 ∙
∙ 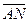 =
= 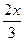
 +
+ 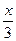
 , где
, где 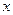 - неизвестное число.
- неизвестное число.
2) 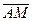 =
= 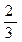
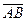 =
= 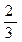
 ,
, 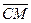 =
= 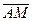 -
- 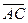 =
= 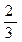
 -
-  ,
, 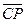 =
= 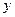
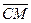 =
= 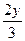
 -
- 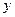
 , где
, где 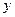 - неизвестное число,
- неизвестное число, 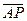 =
= 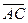 +
+ 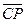 = (1-
= (1- 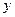 )
)  +
+ 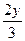
 . В силу единственности разложения вектора по двум заданным неколлинеарным векторам имеем равенства:
. В силу единственности разложения вектора по двум заданным неколлинеарным векторам имеем равенства: 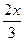 = 1-
= 1- 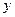 ,
, 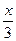 =
= 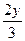 . Отсюда
. Отсюда 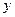 =
= 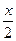 ,
, 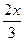 = 1 -
= 1 - 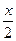 ,
, 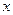 =
= 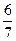 .
.
Следовательно, 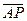 =
= 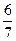
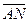 , а поэтому │
, а поэтому │ 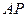 │:│
│:│ 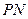 │= 6:1.
│= 6:1.
12. Точки R и Q – проекции точки Р, лежащей на стороне АВ равностороннего треугольника ABC, на его стороны АС и ВС. Доказать, что прямая, содержащая медиану РМ треугольника RQP, проходит через центр О треугольника ABC.
Решение: На рисунке О – точка пересечения медиан AF и BE треугольника ABC.
Покажем, что РМ || РО. По векторной формуле 1 РМ = 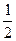 (PQ + PR); заметим, что векторы PQ и BE, PR и AF коллинеарны. Используя условие коллинеарности двух ненулевых векторов, запишем: PQ=хBE, PR =уAF, тогда РМ =
(PQ + PR); заметим, что векторы PQ и BE, PR и AF коллинеарны. Используя условие коллинеарности двух ненулевых векторов, запишем: PQ=хBE, PR =уAF, тогда РМ = 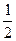 (хВЕ+уAF) (1). По векторной формуле 2 будем иметь ОР =хОВ + уОА, так как QP: BE = АР: АВ =
(хВЕ+уAF) (1). По векторной формуле 2 будем иметь ОР =хОВ + уОА, так как QP: BE = АР: АВ = 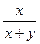 ,
, 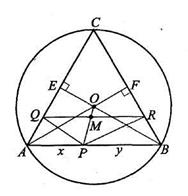
 PR:AF=BP:AB=
PR:AF=BP:AB= 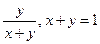 . По свойству медиан треугольника ОВ =-
. По свойству медиан треугольника ОВ =- 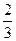 BE, ОА = -
BE, ОА = - 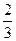 AF, тогда OP =-
AF, тогда OP =- 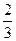 (xBE + yAF) (2), сравнивая равенства (1) и (2), получим РМ =-
(xBE + yAF) (2), сравнивая равенства (1) и (2), получим РМ =- 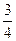 ОР, т. е. векторы РМ и ОР коллинеарны, а значит, прямая, содержащая медиану РМ треугольника RQP, проходит через центр О треугольника ABC.
ОР, т. е. векторы РМ и ОР коллинеарны, а значит, прямая, содержащая медиану РМ треугольника RQP, проходит через центр О треугольника ABC.
13. 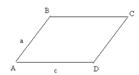 В параллелограмме ABCD
В параллелограмме ABCD 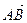 =
=  ,
, 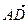 =
= 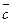 . Выразите векторы
. Выразите векторы 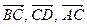 ,
, 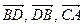 через
через  и
и 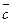 .
.
Решение: ВС=с, CD=-a, AC=a+c, BD=-(a-c), DB=a-c, CA=-(a+c).
14. 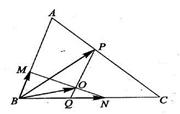 В треугольнике ABC точка М принадлежит стороне АВ,при этом АМ: MB = 2: 1, точки Q, N – на стороне ВС, BQ: QC = 1: 6, BN: NC = 3:2, Р – на стороне АС, АР: PC = 2: 3. Отрезки MN и QP пересекаются в точке О. Найдите МО: ON, РО: OQ.
В треугольнике ABC точка М принадлежит стороне АВ,при этом АМ: MB = 2: 1, точки Q, N – на стороне ВС, BQ: QC = 1: 6, BN: NC = 3:2, Р – на стороне АС, АР: PC = 2: 3. Отрезки MN и QP пересекаются в точке О. Найдите МО: ON, РО: OQ.
Решение: Обозначим МО: ON = β:α; РО:OQ=х:у. По векторной формуле 2* выразим вектор ВО через векторы ВМ и BN, ВО =α ВМ+βBN; так как ВМ= 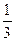 ВА, BN =
ВА, BN = 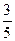 ВС, то ВО=
ВС, то ВО= 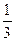 αВА+
αВА+ 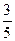 βBC (1); по векторной формуле 2* выразим вектор ВО через векторы BQ и ВР, ВО =xBQ +уВР; так как BQ=
βBC (1); по векторной формуле 2* выразим вектор ВО через векторы BQ и ВР, ВО =xBQ +уВР; так как BQ= 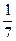 ВС, ВР=ВА+АР; АР=
ВС, ВР=ВА+АР; АР= 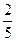 АС; АС=ВС-ВА. ВР=ВА+
АС; АС=ВС-ВА. ВР=ВА+ 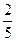 (ВС-ВА)=
(ВС-ВА)= 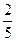 BС+
BС+ 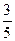 BА, то ВО=(
BА, то ВО=( 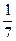 x+
x+ 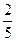 y)BC+
y)BC+ 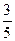 y ВА. (2) Так как вектор ОВ единственным образом раскладывается по неколлинеарным векторам ВС и ВА, то коэффициенты в разложениях (1) и (2) равны, т.е.
y ВА. (2) Так как вектор ОВ единственным образом раскладывается по неколлинеарным векторам ВС и ВА, то коэффициенты в разложениях (1) и (2) равны, т.е. 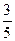 β=
β= 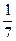 x+
x+ 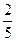 y,
y, 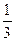 α=
α= 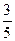 у, заметим, что x+y=1 (3), α+β=1 (4), тогда имеем систему уравнений:
у, заметим, что x+y=1 (3), α+β=1 (4), тогда имеем систему уравнений: 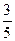 (1-α)=
(1-α)= 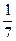 х+
х+ 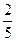 (1 -х),
(1 -х), 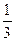 α =
α = 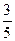 (1-x). Решая эту систему, получим: х =
(1-x). Решая эту систему, получим: х = 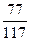 , α =
, α = 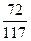 ; учитывая (3) и (4), получим y=
; учитывая (3) и (4), получим y= 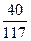 , β=
, β= 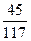 , соответственно х:у = =PO:OQ=
, соответственно х:у = =PO:OQ= 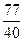 , M0:0N=α:β=
, M0:0N=α:β= 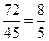 .
.
15. 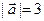 ,
, 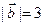 ,
, 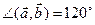 ,
, 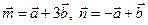 . Найдите косинус угла между векторами m и n.
. Найдите косинус угла между векторами m и n.
Решение. Воспользуемся алгоритмом вычисления угла между векторами:
1. Векторы m и n разложены по базисным векторам а и b.
2. Скалярное произведение векторов m и n будет равно m∙n=(a+3b)(-a+b)=a2-2ab+3b2 = -3.
3. Вычислим длины векторов 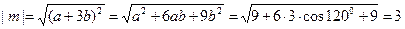 аналогично
аналогично 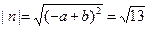 . 4. Тогда cos
. 4. Тогда cos 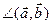 =
= 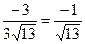 .
.
16. Докажите, что высоты треугольника пересекаются в одной точке.
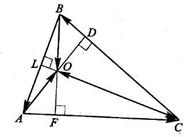 Доказательство. Пусть в ∆ABC проведены высоты AD, BF, CL. Пусть прямые AD и BF пересекаются в точке О. Значит, АО∙СВ = 0 (1), BO∙АС = 0 (2). Покажем, что СО∙BA = 0. Выразим все векторы через векторы СО, СВ и СА. АО=-СА+ СО, ВО=-(ОС+СВ). Сложим равенства (1) и (2), получим: АО∙СВ+ВО∙АС=0 или (-СA+CO)CB-(OC+СВ)АC=CO∙CB-ОС∙AC=СО(СВ-СА)=СО-АВ=0, значит, СО
Доказательство. Пусть в ∆ABC проведены высоты AD, BF, CL. Пусть прямые AD и BF пересекаются в точке О. Значит, АО∙СВ = 0 (1), BO∙АС = 0 (2). Покажем, что СО∙BA = 0. Выразим все векторы через векторы СО, СВ и СА. АО=-СА+ СО, ВО=-(ОС+СВ). Сложим равенства (1) и (2), получим: АО∙СВ+ВО∙АС=0 или (-СA+CO)CB-(OC+СВ)АC=CO∙CB-ОС∙AC=СО(СВ-СА)=СО-АВ=0, значит, СО  АВ, т.е. высоты пересекаются в одной точке.
АВ, т.е. высоты пересекаются в одной точке.
17. В правильном треугольнике ABC со стороной равной 1, отрезок с концами Р и М на сторонах АВ и ВС пересекает отрезок ВК,точка К лежит на стороне АС. Найдите угол между прямыми ВК и РМ,если ВР: РА = 1: 2, ВМ: МС = 3: 1, АК: КС = 1: 2.
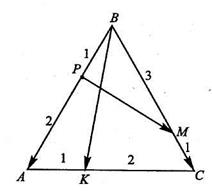 Решение. Воспользуемся алгоритмом вычисления угла между векторами:
Решение. Воспользуемся алгоритмом вычисления угла между векторами:
1. Выразим векторы ВК и РМ через векторы ВА и ВС. ВК= 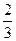 ВС+
ВС+ 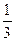 ВА; РМ=ВМ-ВР=
ВА; РМ=ВМ-ВР= 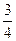 ВС-
ВС- 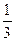 ВА.
ВА.
2. Найдем скалярное произведение этих векторов:
ВК∙РМ=(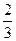 ВС+
ВС+ 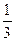 ВА)(
ВА)(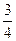 ВС-
ВС- 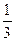 ВА)=
ВА)= 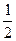 BC2+
BC2+ 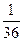 ВА∙СВ-
ВА∙СВ- 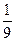 ВА2=
ВА2= 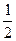 +
+ 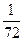 -
- 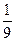 =
= 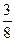 .
.
3. Найдем длины этих векторов:
|BK|2=(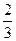 BC+
BC+ 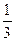 BA)2=
BA)2= 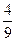 BC2+
BC2+ 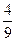 BC∙BA+
BC∙BA+ 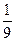 BA2=
BA2= 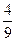 |BC|2+
|BC|2+ 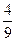 |BC|∙|BA|cos60°+
|BC|∙|BA|cos60°+ 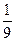 |BA|2=
|BA|2= 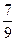 , |BK|=
, |BK|= 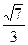 . Аналогично |РМ|2=(
. Аналогично |РМ|2=(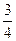 BC-
BC- 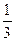 BA)2=
BA)2= 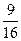 |BC|2-
|BC|2- 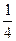 |BC|∙|BA|cos60°+
|BC|∙|BA|cos60°+ 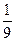 |BA|2=
|BA|2= 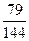 , |РМ|=
, |РМ|= 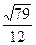 .
.
4. cos 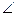 (BK,PM)=
(BK,PM)= 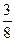 :
: 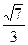 ∙
∙ 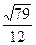 =
= 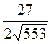 .
.
18. Докажите, что четырехугольник ABCD с вершинами А (1; 0), В (3; 3), С (-1; 2), D (3; 8) – трапеция.
Решение: Нужно показать, что две стороны параллельны: Получим что ВС и AD не параллельны, а AB||CD.
19. Докажите, что для любых а, b, с, d имеет место неравенство 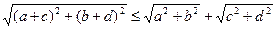 .
.
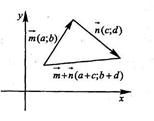
Решение: Рассмотрим векторы m(а;b, n(с;d). Заметим, что (m+n)(а+с;b+d), |m+n|= 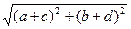 , |m|=
, |m|= 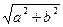 , |n|=
, |n|= 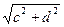 . Сумма векторов m иn равна m +n. По неравенству треугольника будем иметь:
. Сумма векторов m иn равна m +n. По неравенству треугольника будем иметь: 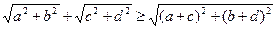 . Равенство достигается в случае, если векторы m и n коллинеарны.
. Равенство достигается в случае, если векторы m и n коллинеарны.
20. При каком значении х векторы 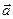 и
и 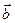 коллинеарны, если
коллинеарны, если 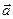 (3- х; 4),
(3- х; 4), 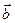 (2; 4 +х).
(2; 4 +х).
Решение: Воспользуемся условием 3.5: для того, чтобы векторы были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны, т.е. 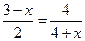 или х 2 + х - 6 = 0, откуда х = -3, х = 2. Ответ: х= —3 или х = 2.
или х 2 + х - 6 = 0, откуда х = -3, х = 2. Ответ: х= —3 или х = 2.
21. Решите неравенство: 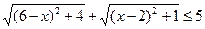 .
.
Решение: Рассмотрим векторы а(6-х; 2), b(х-2; 1), с (4; 3). Заметим, что а + b=с, значит, по неравенству треугольника |а|+|b|≥|с|. Но | a|= 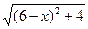 , |b|=
, |b|= 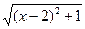 |с| = 5, и тогда
|с| = 5, и тогда 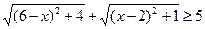 . Следовательно, решением данного неравенства будут только те значения переменной, при которых выполняется равенство
. Следовательно, решением данного неравенства будут только те значения переменной, при которых выполняется равенство 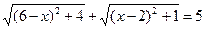 , т. е. | с|=|а|+|b |. Это равенство возможно, если векторы а,b, с коллинеарны (см. задачу 11). По необходимому и достаточному условию коллинеарности двух ненулевых векторов (см. 3.5) будем иметь
, т. е. | с|=|а|+|b |. Это равенство возможно, если векторы а,b, с коллинеарны (см. задачу 11). По необходимому и достаточному условию коллинеарности двух ненулевых векторов (см. 3.5) будем иметь 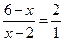 , x=
, x= 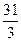 .
.
22. Даны три вектора 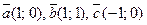 . Найдите такие числа λ и μ, чтобы выполнялось векторное равенство
. Найдите такие числа λ и μ, чтобы выполнялось векторное равенство 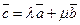 .
.
Решение: 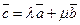 : (-1,0)=λ(1,0)+μ(1,1). Отсюда получаем уравнения: -1=λ+μ, 0=0+μ. Отсюда μ=0, λ=-1.
: (-1,0)=λ(1,0)+μ(1,1). Отсюда получаем уравнения: -1=λ+μ, 0=0+μ. Отсюда μ=0, λ=-1.
23. Даны векторы 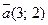 и
и 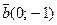 . Найдите абсолютную величину вектора -2
. Найдите абсолютную величину вектора -2  + 4
+ 4  . Ответ: 10.
. Ответ: 10.
24. Найти угол между векторами  и
и  , если |
, если |  |=4, |2
|=4, |2  - 5
- 5  |=17, (3
|=17, (3  + 2
+ 2  ) = 42.
) = 42.
Решение: (3  +2
+2  )(2a-3b)=42, или (3
)(2a-3b)=42, или (3  +2
+2  )(2a-3b)=6a∙a-9a∙b+4a∙b-6b∙b=6a2-5ab-6b2=42. Т.к. a2=|a|2. 6∙16-5ab-6b2=42. 5ab+6b2=54. (1) Аналогично, |2
)(2a-3b)=6a∙a-9a∙b+4a∙b-6b∙b=6a2-5ab-6b2=42. Т.к. a2=|a|2. 6∙16-5ab-6b2=42. 5ab+6b2=54. (1) Аналогично, |2  - 5
- 5  |=(2
|=(2  -5
-5  )(2
)(2  -5
-5  )=289, Или 4a2-10ab-10ab+25b2=289, -4ab+5b2=45. (2) Решая уравнения (1) и (2) получаем, что ab=0, отсюда угол равен 900.
)=289, Или 4a2-10ab-10ab+25b2=289, -4ab+5b2=45. (2) Решая уравнения (1) и (2) получаем, что ab=0, отсюда угол равен 900.
25. 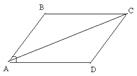 Найдите длину диагонали АС ромба ABCD, у которого длины сторон равны 1 и угол BAD равен 300.
Найдите длину диагонали АС ромба ABCD, у которого длины сторон равны 1 и угол BAD равен 300.
Решение: АС=AB+AD, AC2=AB2+AD2+2AB∙AD, (AB,AD)=|AB||AD|cos300= 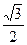 . AC2=2+2
. AC2=2+2 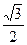 =2+
=2+ 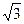 . AC=
. AC= 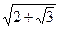 .
.
 2015-06-28
2015-06-28 6382
6382
