Тест чоу на однородность зависимости объясняемой переменной от объясняющих

На практике нередки случаи, когда имеются две выборки пар значений зависимой и объясняющей переменных 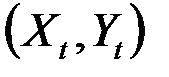. Например, одна выборка пар значений переменных объемом 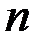получена при одних условиях, а другая, объемом 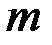, - при несколько измененных условиях. Необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле? Другими словами, можно ли объединить две выборки в одну и рассматривать единую модель регрессии 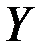по 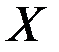(гипотеза )?

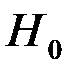Для проверки гипотезы 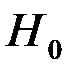применяется тест Чоу (Chow), состоящий в следующем:

1. Используя МНК, построить модель по выборке объемом 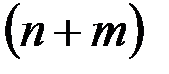и найти для нее .

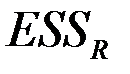2. Пусть есть основание предполагать, что вся выборка состоит из двух подвыборок объемам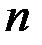и и 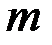соответственно. Для каждой из них строится линейная регрессия. 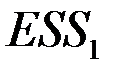- сумма квадратов отклонений значений 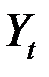от регрессионных значений 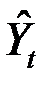, посчитанных по первой подвыборке, 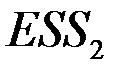– сумма квадратов отклонений значений 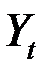от регрессионных значений 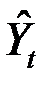, посчитанных по второй подвыборке.

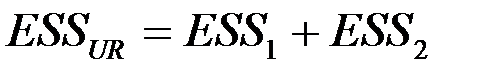
3. Вычислить F – статистику:

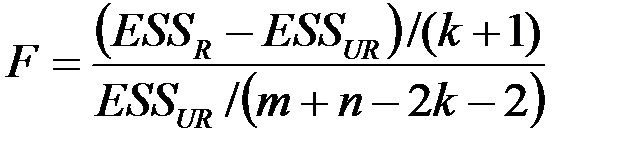где 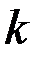– число объясняющих переменных модели.

4. Найти критическую точку распределения Фишера при выбранном уровне значимости .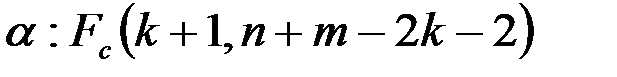

5. Если 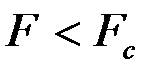, то мы можем объединить две выборки в одну. Если 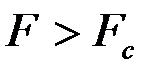, то необходимо использовать две модели.

Проведем тест Чоу на материале примера 2.

Для этих данных в таблице 5 приведены результаты построения модели по первым 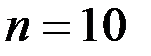наблюдениям.

Таблица 5а.

	df	SS	MS	F	Значимость F
Регрессия		0,1271	0,0212	41,9637	0,0055
Остаток		ESS₁ =0,0015	0,0005
Итого		0,1286

Таблица 5б.

Коэффи-циенты	Стандарт-ная ошибка	t-статис-тика	P-Значение	Нижние 95%	Верхние 95%
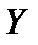-1,4996	0,9134	-1,6417	0,1992	-4,4066	1,4074
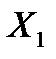0,0004	0,0014	0,3087	0,7777	-0,0040	0,0048
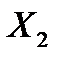0,0001	0,0001	1,0128	0,3857	-0,0002	0,0004
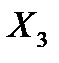0,0155	0,0046	3,3830	0,0430	0,0009	0,0301
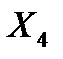0,0085	0,0052	1,6184	0,2040	-0,0082	0,0251
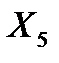0,0007	0,0055	0,1355	0,9008	-0,0167	0,0182
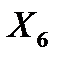0,0069	0,0079	0,8798	0,4437	-0,0182	0,0320

В таблице 6 приведены результаты построения модели по последним 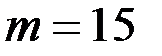наблюдениям. Из таблиц 5 и 6 получаем, что

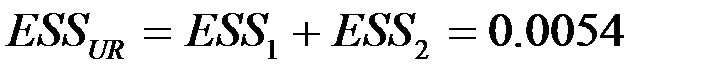
Отчет по модели, построенной по всем 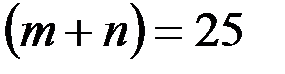наблюдениям, приведен в таблице 3. 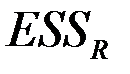данного теста совпадает со значением 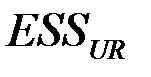таблицы 3, т.е. 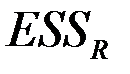= 0.0088.

Считаем статистику 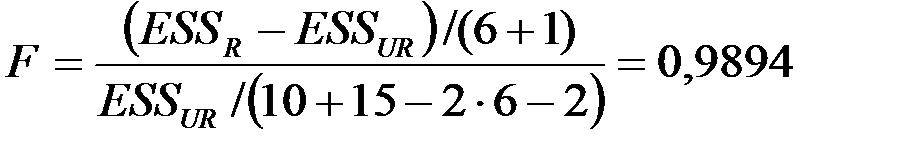и находим табличное значение 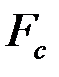= FРАСПОБР(0.05; 7; 11) = 3,0123. Так как 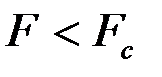, то справедлива гипотеза 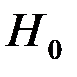, т.е. надо использовать единую модель по всем наблюдениям.

Таблица 6а.

	df	SS	MS	F	Значимость F
Регрессия		0,1126	0,0188	38,6470	0,00002
Остаток		ESS₂ = 0,0039	0,0005
Итого		0,1165

Таблица 6б.

Коэффи-циенты	Стандарт-ная ошибка	t-статис-тика	P-Значение	Нижние 95%	Верхние 95%
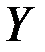-1,4996	0,9134	-1,6417	0,1992	-4,4066	1,4074
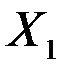0,0004	0,0014	0,3087	0,7777	-0,0040	0,0048
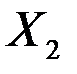0,0001	0,0001	1,0128	0,3857	-0,0002	0,0004
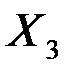0,0155	0,0046	3,3830	0,0430	0,0009	0,0301
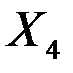0,0085	0,0052	1,6184	0,2040	-0,0082	0,0251
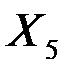0,0007	0,0055	0,1355	0,9008	-0,0167	0,0182
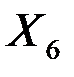0,0069	0,0079	0,8798	0,4437	-0,0182	0,0320

Тесты на гетероскедастичность.

Гомоскедастичность – дисперсия каждого отклонения 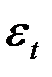одинакова для всех значений .

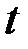Гетероскедастичность – дисперсия объясняемой переменной (а следовательно, и случайных ошибок) не постоянна.

В тестах на гетероскедастичность проверяется основная гипотеза 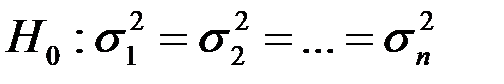(т.е. модель гомоскедастична) против альтернативной гипотезы 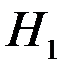: не 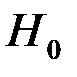(т.е. модель гетероскедастична).