Этот тест применяется, как правило, когда есть предположение о прямой зависимости дисперсии ошибок от величины некоторой объясняющей переменной, входящей в модель.
Предполагается, что 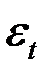 имеет нормальное распределение. Тест включает в себя следующие шаги:
имеет нормальное распределение. Тест включает в себя следующие шаги:
1. Упорядочить данные по убыванию (или по возрастанию) той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2. Исключить 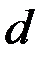 средних (в этом упорядочении) наблюдений (
средних (в этом упорядочении) наблюдений (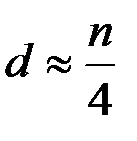 , где
, где 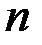 – общее количество наблюдений).
– общее количество наблюдений).
3. Провести две независимых регрессии первых 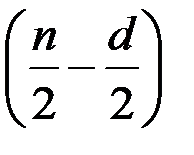 наблюдений и последних
наблюдений и последних 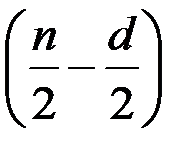 наблюдений и найти, соответственно,
наблюдений и найти, соответственно, 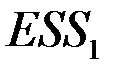 и
и 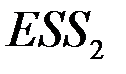 . Из
. Из 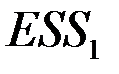 и
и 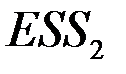 выбираем большую и меньшую величины, соответственно,
выбираем большую и меньшую величины, соответственно, 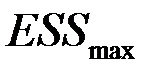 и
и 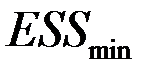 .
.
4. Составить статистику 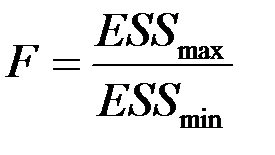 и найти по распределению Фишера
и найти по распределению Фишера 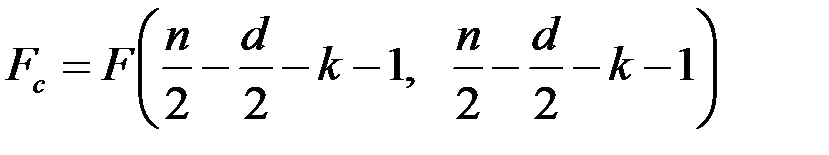 , где
, где 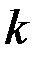 – число объясняющих переменных модели.
– число объясняющих переменных модели.
5. Если 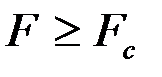 , то гипотеза
, то гипотеза 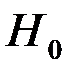 отвергается, т.е. модель гетероскедастична, а если
отвергается, т.е. модель гетероскедастична, а если 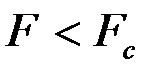 , то гипотеза
, то гипотеза 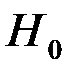 принимается, т.е. модель гомоскедастична.
принимается, т.е. модель гомоскедастична.
Тест проведен для примера 2. Вначале данные упорядочиваем по возрастанию по переменной 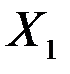 . В данном случае
. В данном случае
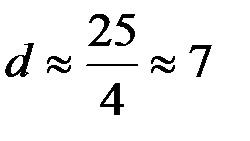 ;
; 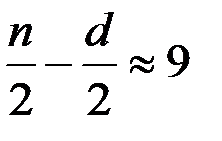
Результаты регрессии, включающей девять первых по переменной 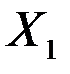 наблюдений, приведены в таблице 7.
наблюдений, приведены в таблице 7.
Таблица 7а.
| df | SS | MS | F | Значимость F | |
| Регрессия | 0,0578 | 0,0096 | 62,8711 | 0,0157 | |
| Остаток | ESS1 = 0,00031 | 0,0002 | |||
| Итого | 0,0581 |
Таблица 7б.
| Коэффи-циенты | Стандарт-ная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
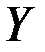 | 0,42833 | 0,20650 | 2,07425 | 0,17376 | -0,46016 | 1,31682 |
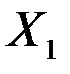 | 0,00112 | 0,00038 | 2,94697 | 0,09844 | -0,00051 | 0,00275 |
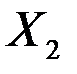 | 0,00003 | 0,00004 | 0,74322 | 0,53479 | -0,00016 | 0,00022 |
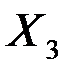 | 0,00805 | 0,00253 | 3,18609 | 0,08599 | -0,00282 | 0,01892 |
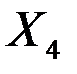 | -0,00322 | 0,00131 | -2,46021 | 0,13303 | -0,00884 | 0,00241 |
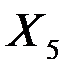 | -0,00075 | 0,00129 | -0,58244 | 0,61919 | -0,00631 | 0,00481 |
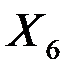 | -0,00424 | 0,00153 | -2,76920 | 0,10941 | -0,01082 | 0,00235 |
Результаты регрессии, включающей последние 9 наблюдений, приведены в таблице 8.
Таблица 8а.
| df | SS | MS | F | Значимость F | |
| Регрессия | 0,1444 | 0,0241 | 397,2778 | 0,0025 | |
| Остаток | ESS2 = 0,00012 | 0,0001 | |||
| Итого | 0,1445 |
Таблица 8б.
| Коэффи-циенты | Стандарт-ная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
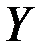 | -0,93944 | 0,08925 | -10,52555 | 0,00891 | -1,32347 | -0,55542 |
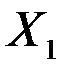 | 0,00018 | 0,00042 | 0,41697 | 0,71719 | -0,00164 | 0,00199 |
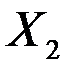 | 0,00004 | 0,00002 | 2,86713 | 0,10316 | -0,00002 | 0,00011 |
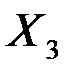 | 0,02215 | 0,00092 | 24,12040 | 0,00171 | 0,01820 | 0,02610 |
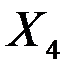 | 0,00035 | 0,00152 | 0,23253 | 0,83775 | -0,00619 | 0,00690 |
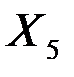 | -0,00025 | 0,00119 | -0,21157 | 0,85204 | -0,00539 | 0,00488 |
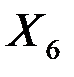 | -0,00186 | 0,00162 | -1,14388 | 0,37112 | -0,00884 | 0,00513 |
Статистика 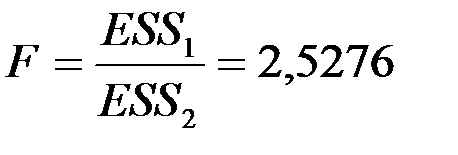 меньше табличного значения
меньше табличного значения 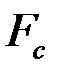 =FРАСПОБР(0.05; 2; 2) = 19, следовательно, модель гомоскедастична.
=FРАСПОБР(0.05; 2; 2) = 19, следовательно, модель гомоскедастична.
 2015-06-28
2015-06-28 1962
1962








