Этот тест используется для обнаружения автокорреляции первого порядка, т.е. проверяется некоррелированность не любых, а только соседних величин 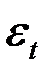 . Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной
. Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной 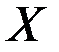 значения
значения 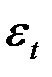 .
.
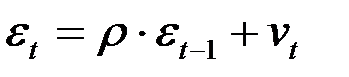
Гипотеза 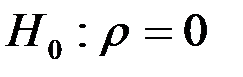 (автокорреляция отсутствует).
(автокорреляция отсутствует).
Общая схема критерия Дарбина – Уотсона следующая:
1. По эмпирическим данным построить уравнение регрессии по МНК и определить значения отклонений 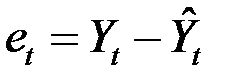 для каждого наблюдения t (t = 1, 2, …, n). (Для этого в диалоговом окне Регрессия установить флажок на функцию Остатки).
для каждого наблюдения t (t = 1, 2, …, n). (Для этого в диалоговом окне Регрессия установить флажок на функцию Остатки).
2. Рассчитать статистику DW:
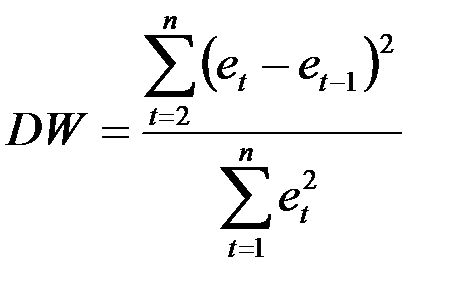
3. По таблице критических точек распределения Дарбина –Уотсона для заданного уровня значимости 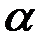 , числа наблюдений
, числа наблюдений 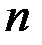 и количества объясняющих переменных
и количества объясняющих переменных 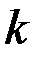 определить два значения:
определить два значения: 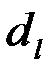 - нижняя граница и
- нижняя граница и 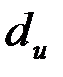 - верхняя граница (таблица 11).
- верхняя граница (таблица 11).
Таблица 11.
| Статистика Дарбина – Уотсона, уровень значимости 0,05 | ||||||||||
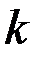 | ||||||||||
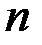 | 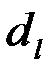 | 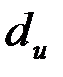 | 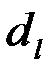 | 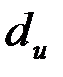 | 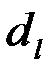 | 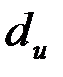 | 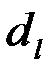 | 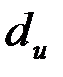 | 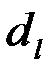 | 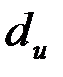 |
| 1,20 | 1,41 | 1,1 | 1,54 | 1,00 | 1,67 | 0,90 | 1,83 | 0,79 | 1,99 | |
| 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,66 | 0,93 | 1,81 | 0,83 | 1,96 | |
| 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 | |
| 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 | |
| 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 | |
| 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 |
4. Сделать выводы по правилу:
|
|
|
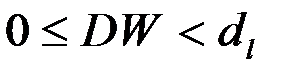 - существует положительная автокорреляция (
- существует положительная автокорреляция (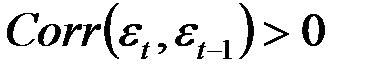 ),
), 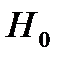 отвергается;
отвергается;
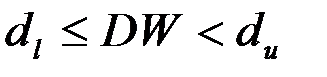 - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
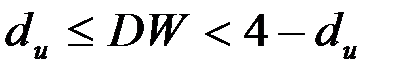 - автокорреляция отсутствует,
- автокорреляция отсутствует, 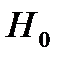 принимается;
принимается;
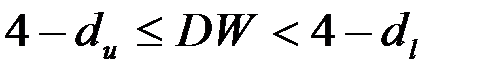 - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
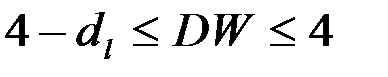 - существует отрицательная автокорреляция (
- существует отрицательная автокорреляция (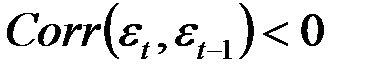 ),
), 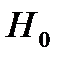 отвергается.
отвергается.
Тест проводится на материале примера 2. Для проведения теста надо поставить флажок «Остатки» в параметрах Регрессии. Отчет по регрессии дан в таблице 3. Отчет по остаткам находится в том же Листе EXCEL и приведен в таблице 12. К этому отчету добавляем столбец значений величин 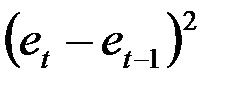 . По этому столбцу считается сумма
. По этому столбцу считается сумма 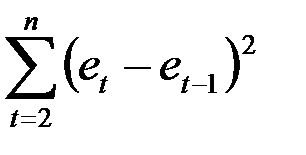 . Сумма
. Сумма 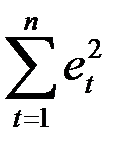 равна
равна 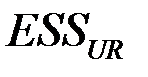 таблицы 3. Таким образом, получаем, что
таблицы 3. Таким образом, получаем, что 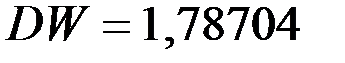 . По таблице при
. По таблице при 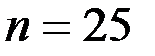 и
и 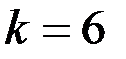 находим
находим 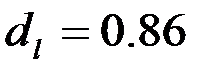 и
и 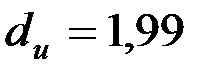 .
.
Следовательно, в рассматриваемом примере 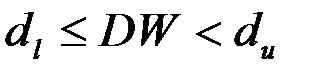 . Таким образом, вывод о наличии автокорреляции не определен.
. Таким образом, вывод о наличии автокорреляции не определен.
Таблица 12.
| Наблюдение | Предсказанное | Остатки 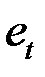 | 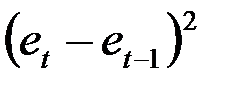 |
| 0,904248 | -0,000248 | ||
| 0,903290 | 0,018710 | 0,000359 | |
| 0,746100 | 0,016900 | 0,000003 | |
| 0,910133 | 0,012867 | 0,000016 | |
| 0,903311 | 0,014689 | 0,000003 | |
| 0,908608 | -0,002608 | 0,000299 | |
| 0,905931 | -0,000931 | 0,000003 | |
| 0,570614 | -0,025614 | 0,000609 | |
| 0,916207 | -0,022207 | 0,000012 | |
| 0,931001 | -0,031001 | 0,000077 | |
| 0,929578 | 0,002422 | 0,001117 | |
| 0,724549 | 0,015451 | 0,000170 | |
| 0,696711 | 0,004289 | 0,000125 | |
| 0,741905 | 0,002095 | 0,000005 | |
| 0,907368 | 0,013632 | 0,000133 | |
| 0,919723 | 0,007277 | 0,000040 | |
| 0,811086 | -0,009086 | 0,000268 | |
| 0,711805 | 0,035195 | 0,001961 | |
| 0,903181 | 0,023819 | 0,000129 | |
| 0,761633 | -0,040633 | 0,004154 | |
| 0,886996 | 0,026004 | 0,004440 | |
| 0,934241 | -0,016241 | 0,001785 | |
| 0,849071 | -0,016071 | 0,000000 | |
| 0,929658 | -0,015658 | 0,000000 | |
| 0,936050 | -0,013050 | 0,000007 | |
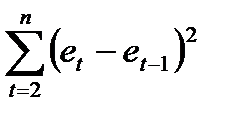 = 0,015716 = 0,015716 |
|
|
|
 2015-06-28
2015-06-28 1933
1933
