Як було сказано в п. 6.1 для завдання графа необхідно занумерувати вершини і ребра, а також задати відношення інцидентності. Відношення інцидентності будемо описувати трьома способами: матрицею інцидентності, матрицею суміжності, списком ребер графа. Опишемо докладно кожний з перерахованих способів.
Матриця інцидентності 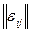 – це матриця розміром
– це матриця розміром 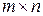 , де вертикально вказуються вершини
, де вертикально вказуються вершини 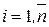 , а горизонтально – ребра
, а горизонтально – ребра 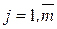 . На перетині
. На перетині 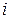 -того і
-того і 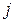 -того рядків число
-того рядків число 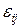 дорівнює:
дорівнює:
а) у випадку неорієнтованого графа
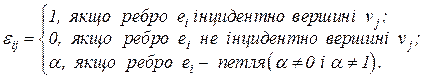
б) у випадку орієнтованого графа
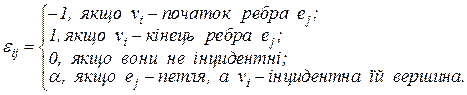
Матриця суміжності 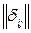 ‑ це квадратна матриця розміром
‑ це квадратна матриця розміром 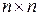 , де
, де
вертикально і горизонтально вказуються вершини графа 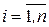 і
і 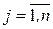 . На перетинанні
. На перетинанні 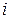 -того і
-того і 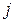 -того рядків число
-того рядків число 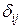 дорівнює:
дорівнює:
‑ числу ребер, що з'єднують ці вершини у випадку неорієнтованого графа;
‑ числу ребер з початком в 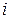 -тій вершині і кінцем в
-тій вершині і кінцем в 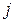 -тій вершині у випадку орієнтованого графа.
-тій вершині у випадку орієнтованого графа.
Список ребер графа – це таблиця, що складається із трьох рядків. У першому перераховані всі ребра; у другому і третьому – інцидентні їм вершини:
‑ у випадку неорієнтованого графа порядок вершин у рядку довільний;
‑ у випадку орієнтованого графа першою записується вершина, де починається ребро (другий рядок); вершина, де закінчується ребро, записується у третій рядок.
Для нумерації вершин і ребер графа використовують різний символьний запис: римські, арабські цифри, латинські букви.
Якщо графи рівні, то їх матриці суміжності і інцидентності, а також список ребер, однакові.
Приклад 6.9. Задати матрицями інцидентності і суміжності, а також списком ребер, неорієнтований граф, зображений на рис. 6.13.
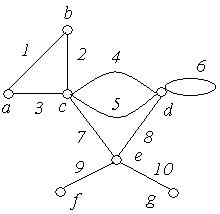
Рис. 6.13.
Рішення:
Матриця інцидентності Матриця суміжності
 | 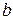 |  |  |  | 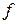 | 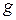 | |||||||||||||
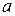 | 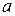 | ||||||||||||||||||
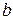 | 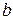 | ||||||||||||||||||
 |  | ||||||||||||||||||
 |  | ||||||||||||||||||
 |  | ||||||||||||||||||
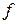 | 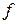 | ||||||||||||||||||
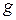 | 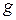 |
Тут 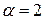 .
.
Список ребер
| Ребро | |||||||||||
| Вершини | початок | a | b | a | c | c | d | c | d | e | e |
| кінець | b | c | c | d | d | d | e | e | f | g |
Як бачимо, у кожному стовпці матриці інцидентності є тільки два елементи, відмінних від нуля (або один, якщо ребро – петля).
Матриця суміжності симетрична щодо головної діагоналі.
Список ребер є найбільш компактним способом завдання графів.
Кожний із наданих способів однозначно описує граф, зображений на рис. 6.13.
Приклад 6.10. Задати матрицями інцидентності, суміжності, списком ребер орієнтований граф, зображений на рис. 6.14.
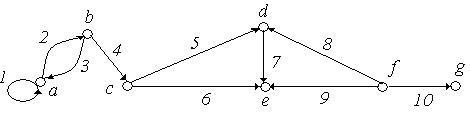
Рис. 6.14.
Рішення:
Матриця інцидентності
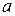 | 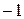 | |||||||||
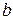 | 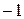 | 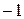 | ||||||||
 | 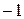 | 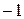 | ||||||||
 | 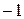 | |||||||||
 | ||||||||||
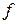 | 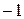 | 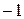 | 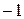 | |||||||
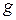 |
Матриця суміжності
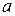 | 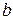 |  |  |  | 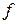 | 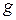 | |
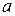 | |||||||
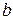 | |||||||
 | |||||||
 | |||||||
 | |||||||
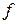 | |||||||
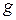 |
Список ребер
| Ребро | |||||||||||
| Вершини | початок | a | a | b | b | c | c | d | f | f | f |
| кінець | a | b | a | c | d | e | e | d | e | g |
Відмінність матриці інцидентності орієнтованого графа від неорієнтованого складається у вказівці початку і кінця ребер. Матриця суміжності губить свою симетричність. У списку ребер важливий порядок вказівки вершин, що з'єднують зазначеним ребром (від початку до кінця).
Як відзначалося вище, всі розглянуті способи завдання графів однозначно визначають граф. Виникає питання: чи можливо відновити граф по заданих матрицях інцидентності, суміжності або списку ребер? Очевидна позитивна відповідь.
По матриці інцидентності число ребер і вершин визначається з розмірності матриці: число ребер 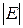 графа дорівнює числу стовпців
графа дорівнює числу стовпців 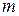 , а число вершин
, а число вершин 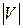 ‑ числу рядків
‑ числу рядків 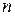 матриці.
матриці.
По матриці суміжності число вершин визначається з розмірності матриці. Як було відзначено, матриця суміжності н-графа симетрична щодо головної діагоналі, і кількість ребер визначається верхнім правим трикутником матриці, розташованим над головною діагоналлю, включаючи останню. Тобто, число ребер н-графа дорівнює сумі елементів, розташованих на головній діагоналі і у верхньому правому трикутнику. У матриці суміжності орграфа симетрія відсутня, а число ребер дорівнює сумі всіх елементів матриці суміжності.
Список ребер є скороченим варіантом матриці інцидентності. Кількість ребер очевидна, а кількість вершин дорівнює максимальному номеру всіх перерахованих вершин зі списку.
Тобто, матриця інцидентності і список ребер по суті, еквівалентні, то знаючи матрицю інцидентності можна записати список ребер, і навпаки.
Побудова матриці інцидентності за списком ребер. Кожен рядок списку ребер відповідає рядку в матриці інцидентності з тим же номером. Для неорієнтованого графа в кожному рядку списку ребер зазначені номери елементів матриці інцидентності, рівні 1 (всі інші елементи – нулі). Для орієнтованого графа першою вказується вершина, що відповідає початку ребра (у матриці інцидентності – елемент 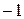 ), а другий – відповідному кінцю ребра (у матриці інцидентності – елемент 1). При збігу елементів у рядку списку ребер, у відповідному рядку матриці інцидентності записується число, відмінне від
), а другий – відповідному кінцю ребра (у матриці інцидентності – елемент 1). При збігу елементів у рядку списку ребер, у відповідному рядку матриці інцидентності записується число, відмінне від 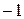 , 0, 1, наприклад, 2. Така ситуація відповідає наявності у графі петель.
, 0, 1, наприклад, 2. Така ситуація відповідає наявності у графі петель.
Приклад 6.11. Побудувати матрицю інцидентності неорієнтованого графа за списком ребер:
| Ребро | |||||||||
| Вершини | початок | a | d | e | c | a | d | b | f |
| кінець | d | f | f | e | b | c | f | f |
Рішення:
Матриця інцидентності, відповідно до списку ребер, має вигляд:
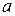 | ||||||||
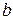 | ||||||||
 | ||||||||
 | ||||||||
 | ||||||||
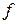 |
Приклад 6.12. Запиcати список ребер відповідно до матриці інцидентності орієнтованого графа:
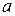 | 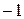 | |||||||
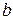 | 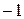 | 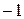 | ||||||
 | 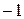 | |||||||
 | 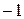 | |||||||
 | 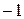 | |||||||
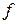 |
Рішення:
Список ребер, записаний відповідно до матриці інцидентності орієнтованого графа має вигляд:
| Ребро | |||||||||
| Вершини | початок | b | b | c | c | d | d | e | a |
| кінець | a | c | c | d | d | e | f | f |
У визначенні 6.14 уведене поняття ізоморфних графів. Чи можливо встановити, чи є графи ізоморфними за їхніми матрицями інцидентності, суміжності, або списку ребер?
Для перевірки ізоморфності графів 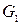 і
і 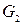 за матрицею суміжності необхідно визначити, чи існує така перестановка рядків і стовпців у матриці суміжності
за матрицею суміжності необхідно визначити, чи існує така перестановка рядків і стовпців у матриці суміжності 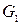 , щоб у результаті вийшла матриця
, щоб у результаті вийшла матриця 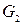 . Із цією метою треба зробити всі можливі перестановки рядків і стовпців (а їхня максимальна кількість дорівнює
. Із цією метою треба зробити всі можливі перестановки рядків і стовпців (а їхня максимальна кількість дорівнює 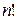 ∙
∙ 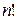 )! Якщо після однієї із цих перестановок матриці суміжності тотожньо збіжаться, то графи ізоморфні.
)! Якщо після однієї із цих перестановок матриці суміжності тотожньо збіжаться, то графи ізоморфні.
Для перевірки ізоморфності графів 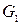 і
і 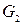 за матрицею інцидентності (і списку ребер) необхідно визначити, чи існує така перестановка рядків і стовпців у матриці інцидентності
за матрицею інцидентності (і списку ребер) необхідно визначити, чи існує така перестановка рядків і стовпців у матриці інцидентності 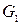 , щоб у результаті вийшла матриця
, щоб у результаті вийшла матриця 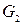 . Із цією метою треба зробити всі можливі пари перестановок рядків і стовпців (а їхня максимальна кількість дорівнює
. Із цією метою треба зробити всі можливі пари перестановок рядків і стовпців (а їхня максимальна кількість дорівнює 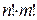 )! Якщо після однієї із цих перестановок матриці інцидентності тотожно збіжаться, то графи ізоморфні.
)! Якщо після однієї із цих перестановок матриці інцидентності тотожно збіжаться, то графи ізоморфні.
І в першому, і в другому випадку це досить трудомісткі операції, і рішення задачі “вручну” не завжди виправдано. Найчастіше изоморфність графів простіше встановити з їх графічних подань.
Вправи:
1. Задати матрицями інцидентності, суміжності і списком ребер неорієнтовані графи, зображені на рис. 6.15:
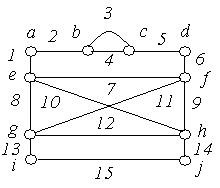
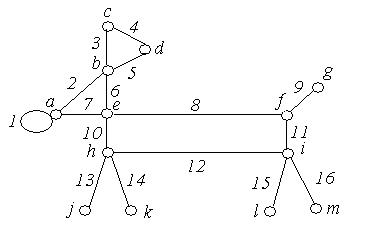
(а) (б)
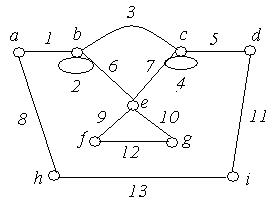
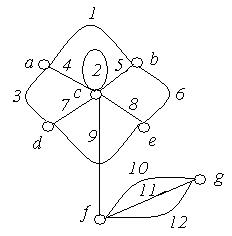
(в) (г)
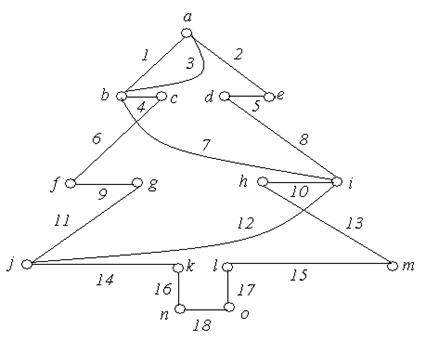
(д)
Рис. 6.15.
2. Задати матрицями інцидентності, суміжності і списком ребер орієнтовані графи, зображені на рис. 6.16:
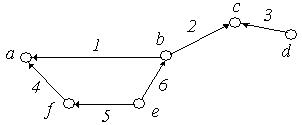
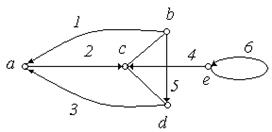
(а) (б)
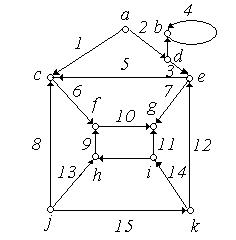
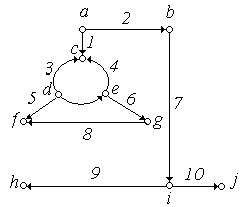
(в) (г)
Рис. 6.16.
3. Для заданих матриць інцидентності а) і б) знайти відповідний граф.
а) б)
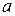 | 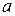 | |||||||||||||||||
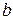 | 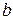 | |||||||||||||||||
 |  | |||||||||||||||||
 |  | |||||||||||||||||
 |  |
4. Для заданих матриць суміжності а) і б) знайти відповідний граф.
а) б)
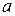 | 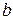 |  |  |  | 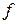 | 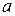 | 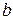 |  |  |  | 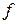 | |||||
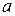 | 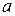 | |||||||||||||||
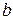 | 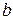 | |||||||||||||||
 |  | |||||||||||||||
 |  | |||||||||||||||
 |  | |||||||||||||||
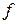 | 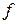 |
 2015-06-28
2015-06-28 3584
3584








