В 1857 році математик Вільям Роуен Гамільтон придумав іграшку-головоломку. Ця іграшка являла собою додекаедр – правильний багатогранник, 12 граней якого − це правильні п'ятикутники. У кожному з 20 кутів просвердлувалась дірка, у яку вставляли кілочок, що зображував місто. За допомогою мотузки було потрібно знайти шлях через міста, відвідав кожне місто один раз, і повернутися у вихідне місто. Додекаедр на площині зображується так, як показано на рис. 6.38.
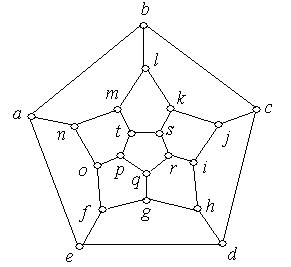
Рис. 6.38.
Задача головоломки зводиться до знаходження циклу в графі, що проходить через кожну вершину, крім початкової, тільки один раз.
Визначення 6.45. Шляхом Гамільтона (або гамільтоновим ланцюгом) називається простий ланцюг, що проходить через всі вершини графа, з початком і кінцем у різних вершинах 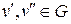 .
.
Визначення 6.46. Цикл Гамільтона ‑ це простий цикл, що проходить через всі вершини графа  .
.
Гамільтонів цикл у деякому змісті протилежний ейлерову циклу, що проходить через всі ребра один раз, хоча до певного моменту обидва цикли можуть здаватися схожими. Цикл Гамільтона виявляється набагато складніше, і для його знаходження поки немає ефективних алгоритмів, що вимагають істотно меншого часу, чим пряме перебирання варіантів. Проте приведемо ряд теорем без доведення, що дозволяють нам судити про можливість відшукати гамільтонів цикл у досліджуваному графі. А для початку покажемо один з варіантів рішення головоломки, запропонованої Гамільтоном (рис. 6.39).
Рис. 6.39.
Теорема 6.5. Для будь-якої вершини із циклу Гамільтона існує рівно два ребра із цього циклу, інцидентні даній вершині.
Визначення 6.47. Граф, що має цикл Гамільтона, називається гамільтонів.
Виходячи з наведеного визначення, як наслідок теореми 6.5, робимо висновок про те, що будь-який граф, що має вершину степені 1, не є гамільтонів. Помітимо також, що для того, щоб граф мав цикл Гамільтона, необхідно, щоб він був зв'язним.
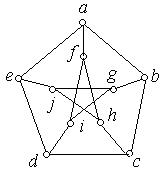
Приклад 6.23. Граф Петерсона, зображений на рис. 6.40,а, має шлях Гамільтона (рис. 6.40,б), але не має цикл Гамільтона.
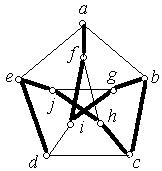
(а) (б)
Рис. 6.40.
Теорема 6.6. Якщо граф  має ребро розрізу, то він не може мати цикл Гамільтона. Якщо компоненти графа, отримані шляхом видалення ребра розрізу, мають цикл Гамільтона, то граф
має ребро розрізу, то він не може мати цикл Гамільтона. Якщо компоненти графа, отримані шляхом видалення ребра розрізу, мають цикл Гамільтона, то граф  має шлях Гамільтона.
має шлях Гамільтона.
Теорема 6.7. Якщо  ‑ зв'язний граф з
‑ зв'язний граф з 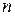 вершинами
вершинами 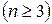 і для кожної пари несуміжних вершин
і для кожної пари несуміжних вершин 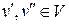 , сума степенів вершин задовольняє умові
, сума степенів вершин задовольняє умові 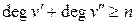 , тоді граф
, тоді граф  має цикл Гамільтона.
має цикл Гамільтона.
З теореми 6.7 випливає наслідок, більш відомий, чим сама теорема.
Наслідок. Якщо  ‑ зв'язний граф з
‑ зв'язний граф з 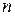 вершинами
вершинами 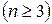 і для кожної
і для кожної
вершини 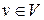 виконується умова
виконується умова 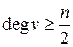 , то граф
, то граф  має цикл Гамільтона.
має цикл Гамільтона.
Приклад 6.24. Знайдіть цикл Гамільтона, якщо він існує, для графа  , зображеного на рис. 6.41,а.
, зображеного на рис. 6.41,а.
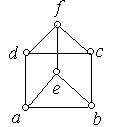
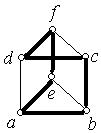
(а) (б)
Рис. 6.41.
Рішення: Граф  ‑ зв'язний, кількість вершин графа –
‑ зв'язний, кількість вершин графа – 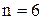 . Степінь кожної з вершин дорівнює 3, тобто кожна з вершин графа задовольняє умові
. Степінь кожної з вершин дорівнює 3, тобто кожна з вершин графа задовольняє умові 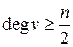 . Отже, даний граф є гамільтонів, тобто існує цикл Гамільтона. Знайти
. Отже, даний граф є гамільтонів, тобто існує цикл Гамільтона. Знайти
його можемо тільки методом перебирання. Результати прямого перебирання – цикл 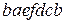 (рис. 6.41,б).
(рис. 6.41,б).
Практичне застосування циклів Гамільтона знаходимо в рішенні класичної задачі комівояжера, яка цікава для людей, у чиє коло обов'язків входить знаходження оптимальних шляхів, наприклад, об'їзду філій фірми, транспортування вантажів, доставки товарів і інше.
Задача комівояжера. Комівояжер повинен відвідати кілька міст і повернутися у вихідний пункт. Відстані між містами відомі. Потрібно знайти дорогу найкоротшої довжини. При такій постановці задачі схема доріг являє собою граф, у якій будь-якому ребру 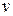 запропонована певна довжина
запропонована певна довжина 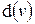 . Задача комівояжера зводиться до знаходження в отриманому графі із заданими довжинами ребер циклу Гамільтона
. Задача комівояжера зводиться до знаходження в отриманому графі із заданими довжинами ребер циклу Гамільтона 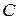 мінімальної довжини.
мінімальної довжини.
Існує ряд алгоритмів, досить громіздких, що дозволяють знаходити найкоротший шлях від вершини 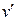 до вершини
до вершини 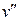 , таких як алгоритми Дейкстри, Флойда-Уоршолла і т.п. Але ефективних алгоритмів, для пошуку циклу Гамільтона мінімальної довжини немає. Через їхню відсутність, щораз цю практичну задачу доводиться вирішувати методом прямого перебирання.
, таких як алгоритми Дейкстри, Флойда-Уоршолла і т.п. Але ефективних алгоритмів, для пошуку циклу Гамільтона мінімальної довжини немає. Через їхню відсутність, щораз цю практичну задачу доводиться вирішувати методом прямого перебирання.
Вправи:
1. Знайдіть цикл Гамільтона, якщо він існує, для кожного з наведених графів. Рис. 6.42, а) − е).
а) б) в)
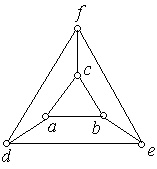
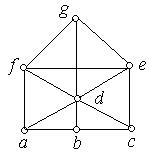
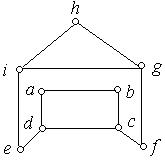
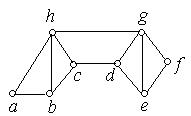
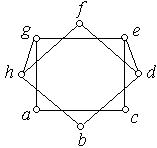
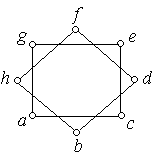 г) д) е)
г) д) е)
ж) з) к)
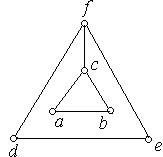
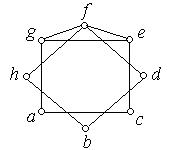
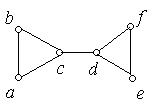
Рис. 6.42.
2. Знайдіть шлях Гамільтона, якщо він існує, для кожного з наведених графів. Рис. 6.42, ж) – к).
Планарні графи
Визначення 6.48. Граф  називається правильно укладеним на площині, якщо його графічне подання таке, що ребра графа перетинаються тільки в його вершинах.
називається правильно укладеним на площині, якщо його графічне подання таке, що ребра графа перетинаються тільки в його вершинах.
Визначення 6.49. Граф  називається плоским (планарним), якщо він ізоморфний деякому графу
називається плоским (планарним), якщо він ізоморфний деякому графу 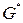 , правильно укладеному на площині. Тобто плоский граф – це граф, який можна правильно укласти на площині.
, правильно укладеному на площині. Тобто плоский граф – це граф, який можна правильно укласти на площині.
Приклад 6.25. Графи 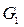 і
і 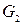 , подані на рис. 6.43, ізоморфні. Граф
, подані на рис. 6.43, ізоморфні. Граф 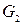 ‑ правильно укладений на площині. Отже, дані графи - плоскі.
‑ правильно укладений на площині. Отже, дані графи - плоскі.
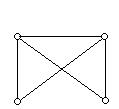
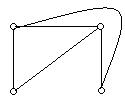
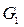
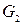
Рис. 6.43.
Розглянемо граф як малюнок на аркуші паперу. Якщо граф планарний, тобто намальований так, що його ребра не перетинаються, і його необхідно розрізати уздовж ребер, то граф виявиться розділеним на частини, включаючи зовнішню частину. Такі частини називаються гранями. Границя кожної грані є циклом.
Визначення 6.50. Гранню планарного графа називається така максимальна ділянка площини, що будь-які дві її точки можуть бути з'єднані кривою, що не перетинає ребро графа.
Задача про можливості правильного укладання графа на площині є актуальною у зв'язку з використанням у радіотехніці друкованих схем. Інтегральні мікросхеми складаються із шарів мініатюрних мікросхем, удрукованих у пластину. Ці схеми наносяться на ізолятор у друкований спосіб і перетинання яких-небудь двох провідників, у непередбачуваних точках (не у вершинах графа), привело б до їх замикання. Тобто для друкування електричних схем просто необхідно, щоб графи (що їх зображують) були плоскими.
Задачі, пов'язані із плоскими графами, актуальні не тільки в радіотехніці. Приведемо класичну задачу про три міста і три джерела постачання. Нехай є три міста 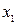 ,
, 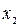 і
і 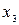 і три джерела життєзабезпечення: водонапірна башта
і три джерела життєзабезпечення: водонапірна башта 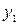 , електростанція
, електростанція 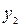 і станція магістрального газопроводу
і станція магістрального газопроводу 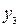 . Чи можна з'єднати ці міста із джерелами постачання водою, газом і електрикою так, щоб траншеї, прориті для цих ліній (на одній глибині) не перетиналися?
. Чи можна з'єднати ці міста із джерелами постачання водою, газом і електрикою так, щоб траншеї, прориті для цих ліній (на одній глибині) не перетиналися?
Ця задача зводиться до побудови плоского графа, ізоморфного графу, зображеному на рис. 6.44.
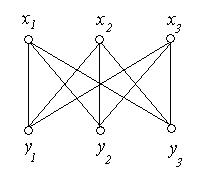
Рис. 6.44.
Відповідь на питання поставлене у сформульованій задачі негативна. Завжди можна намалювати 8 попарно неперетинаючихся ліній, а дев'ята обов'язково перетне одну із цих восьми.
Доведення неможливості такої побудови спирається на теорему, доведену Жорданом. Проілюструємо її в такий спосіб. Нехай 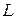 ‑ безперервна замкнута лінія без самоперетинань (рис. 6.45). Ця лінія ділить площину на дві частини: зовнішню і внутрішню. Будь-які дві точки
‑ безперервна замкнута лінія без самоперетинань (рис. 6.45). Ця лінія ділить площину на дві частини: зовнішню і внутрішню. Будь-які дві точки 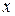 і
і 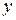 із внутрішньої і зовнішньої частин відповідно можна з'єднати тільки лінією, що перетинає
із внутрішньої і зовнішньої частин відповідно можна з'єднати тільки лінією, що перетинає 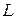 .
.
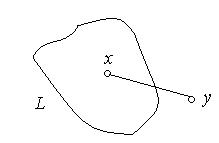
Рис. 6.45.
Позначимо граф, зображений на рис. 6.44 як 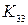 . Замінимо граф
. Замінимо граф 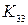 йому ізоморфним (рис. 6.46).
йому ізоморфним (рис. 6.46).
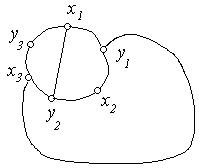
Рис. 6.46.
З'єднати вершини 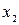 і
і 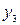 без перетинання вже проведених ребер неможливо, тому що точка
без перетинання вже проведених ребер неможливо, тому що точка 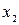 лежить усередині області, обмеженої кривою
лежить усередині області, обмеженої кривою 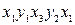 , а точка
, а точка 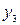 ‑ поза зазначеної області. Отже, граф
‑ поза зазначеної області. Отже, граф 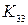 не є планарным.
не є планарным.
Аналогічно доводиться непланарність повного графа 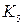 (рис. 6.47).
(рис. 6.47).
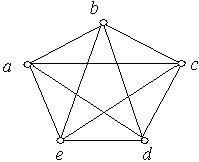
Рис. 6.47.
Використовуючи графи 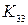 і
і 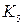 , можна сформулювати наступний критерій планарності графів.
, можна сформулювати наступний критерій планарності графів.
Теорема 6.7. (Теорема Куратовського). Граф є планарним тоді і тільки тоді, коли він не містить підграф, ізоморфний графу 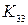 або
або 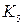 .
.
Існують і інші критерії планарності графів.
Теорема 6.8. Якщо  ‑ зв'язний планарний граф, що містить
‑ зв'язний планарний граф, що містить 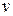 вершин,
вершин,  ребер і
ребер і 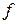 граней, то повинна виконуватися умова
граней, то повинна виконуватися умова 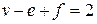 .
.
За допомогою теореми 6.8 задача про життєзабезпечення трьох будинків (рис. 6.44) вирішується в такий спосіб. У графа 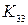 шість вершин і дев'ять ребер:
шість вершин і дев'ять ребер: 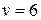 ,
, 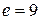 , а кількість граней ‑
, а кількість граней ‑ 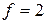 . Підставимо в умову
. Підставимо в умову  . Умова теореми 6.8 не виконується. Отже, граф
. Умова теореми 6.8 не виконується. Отже, граф 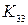 ‑ не планарний.
‑ не планарний.
Лема 6.1. У довільному планарному графі  з кількістю вершин не менше трьох має місце нерівність
з кількістю вершин не менше трьох має місце нерівність 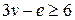 .
.
За допомогою леми 6.1 доведемо, що граф 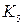 не планарний. Граф
не планарний. Граф 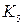 має п'ять вершин і десять ребер:
має п'ять вершин і десять ребер: 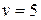 ,
, 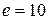 . Скористаємося умовою
. Скористаємося умовою 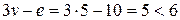 . Як бачимо, умова
. Як бачимо, умова 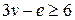 для графа
для графа 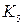 не виконана, отже, граф
не виконана, отже, граф 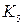 не планарний.
не планарний.
Вправи:
1. Кожний з наведених на рис. 6.48 a) − i) графів перевірити на планарність. Аргументувати рішення.
а) б) в)
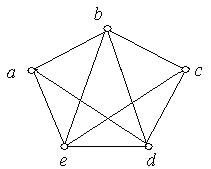
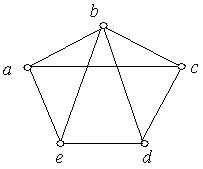
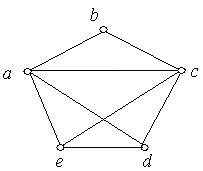
г) д) е)
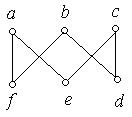
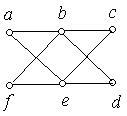
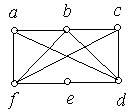
ж) з) і)
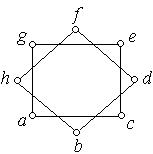
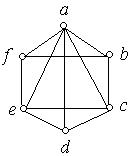
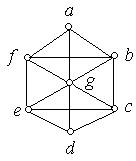
Рис. 6.48.
2. Для кожного планарного графа із завдання 1 запропонувати правильне укладання його на площині.
3. Для кожного планарного графа із завдання 1 перевірити виконання умови 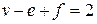 .
.
 2015-06-28
2015-06-28 4439
4439








