6.3.1.  ‑неорієнтований граф
‑неорієнтований граф
Визначення 6.16. Маршрутом (шляхом) у графі  називається така послідовність ребер
називається така послідовність ребер 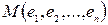 , у якій кожні два сусідніх ребра
, у якій кожні два сусідніх ребра 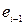 і
і 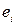 мають загальну вершину. У маршруті те саме ребро може зустрічатися кілька разів. Іншими словами маршрут – це сукупність ребер, які об'єднані разом вершинами так, що можна рухатися по них уздовж графа.
мають загальну вершину. У маршруті те саме ребро може зустрічатися кілька разів. Іншими словами маршрут – це сукупність ребер, які об'єднані разом вершинами так, що можна рухатися по них уздовж графа.
Визначення 6.17. Початок маршруту – це вершина 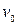 , інцидентна ребру
, інцидентна ребру 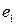 і не інцидентна ребру
і не інцидентна ребру 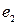 . Кінець маршруту – це вершина
. Кінець маршруту – це вершина 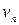 інцидентна ребру
інцидентна ребру 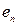 і не інцидентна
і не інцидентна 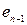 . Якщо ребра
. Якщо ребра 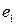 ,
, 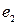 (
(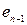 ,
, 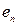 ) ‑ кратні, то необхідно додатково вказувати, яку із двох інцидентних вершин вважати початком (кінцем) маршруту.
) ‑ кратні, то необхідно додатково вказувати, яку із двох інцидентних вершин вважати початком (кінцем) маршруту.
Визначення 6.18. Маршрут довжини 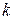 ‑ послідовність, що містить
‑ послідовність, що містить 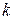 ребер. Іншими словами, довжиною маршруту називається кількість ребер у ньому; при цьому кожне ребро враховується стільки разів, скільки разів воно зустрічається в маршруті.
ребер. Іншими словами, довжиною маршруту називається кількість ребер у ньому; при цьому кожне ребро враховується стільки разів, скільки разів воно зустрічається в маршруті.
Позначення маршруту з 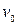 у
у 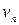 ‑ послідовністю
‑ послідовністю 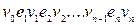 надлишкове, тому ми будемо позначати маршрут як
надлишкове, тому ми будемо позначати маршрут як 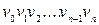 .
.
Визначення 6.19. Маршрут, всі ребра якого різні, називається ланцюгом. Ланцюг, що не перетинає себе, тобто не має вершин, що повторюються, називається простим.
Приклад 6.13. Визначити можливі маршрути (і їхню довжину) з вершини 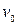 в
в 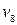 у графі, зображеному на рис. 6.17.
у графі, зображеному на рис. 6.17.
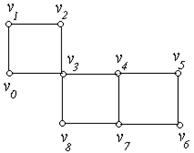
Рис. 6.17
Рішення: з вершини 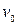 у
у 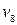 ведуть, наприклад, шляхи:
ведуть, наприклад, шляхи:
1) 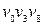 ‑ довжини 2; 5)
‑ довжини 2; 5) 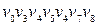 ‑ довжини 6;
‑ довжини 6;
2) 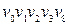 ‑ довжини 4; 6)
‑ довжини 4; 6) 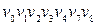 ‑ довжини 6;
‑ довжини 6;
3) 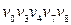 ‑ довжини 4; 7)
‑ довжини 4; 7) 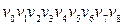 ‑ довжини 8;
‑ довжини 8;
4) 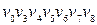 ‑ довжини 6; 8)
‑ довжини 6; 8) 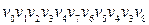 ‑ довжини 10.
‑ довжини 10.
Шляхи: 6), 8) не є простими.
Визначення 6.20. Маршрут, у якому збігаються початок і кінець ‑ 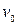 і
і 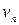 ‑ називається циклічним. Циклічний маршрут називається циклом, якщо він є ланцюг, і простим циклом – якщо це простий ланцюг.
‑ називається циклічним. Циклічний маршрут називається циклом, якщо він є ланцюг, і простим циклом – якщо це простий ланцюг.
Наприклад, маршрут 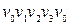 для графа, зображеного на рис. 6.17, є простим циклом; а маршрут
для графа, зображеного на рис. 6.17, є простим циклом; а маршрут 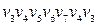 є циклом, але не буде простим, тому що містить вершини, які повторюються.
є циклом, але не буде простим, тому що містить вершини, які повторюються.
Визначення 6.21. Вершини 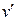 і
і 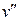 графа
графа  називаються зв'язаними, якщо існує маршрут з початком у
називаються зв'язаними, якщо існує маршрут з початком у 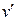 і кінцем у
і кінцем у 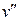 . Маршрут між зв'язаними вершинами може бути поданий простим ланцюгом.
. Маршрут між зв'язаними вершинами може бути поданий простим ланцюгом.
Визначення 6.22. Граф  називається зв'язним, якщо будь-які пари його вершин зв'язані між собою.
називається зв'язним, якщо будь-які пари його вершин зв'язані між собою.
Приклад 6.14. Граф, зображений на рис. 6.18,а – не зв'язний, а граф на рис. 6.18,б – зв'язний.
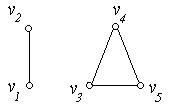
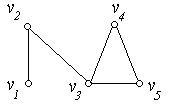
(а) (б)
Рис. 6.18
Теорема 6.3. Якщо існує маршрут з вершини 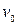 в
в 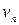 графа
графа  , то існує простий ланцюг, що з'єднує вершини
, то існує простий ланцюг, що з'єднує вершини 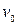 і
і 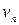 .
.
Наслідок. Граф  є зв'язним тоді і тільки тоді, коли між будь-якими двома його вершинами існує простий ланцюг.
є зв'язним тоді і тільки тоді, коли між будь-якими двома його вершинами існує простий ланцюг.
Визначення 6.23. Максимальний непустий зв'язний підграф 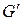 графа
графа  називається компонентом графа
називається компонентом графа  .
.
Отже, кожен граф являє собою об'єднання своїх компонент, які попарно не перетинаються.
Незв'язний граф має, як мінімум, два компоненти. Наприклад, граф, зображений на рис. 6.18,а, має два компоненти: 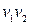 і
і 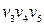 .
.
Визначення 6.24. Вершина 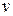 називається точкою зчленування, якщо видалення її із графа приводить до збільшення числа компонент зв’язності.
називається точкою зчленування, якщо видалення її із графа приводить до збільшення числа компонент зв’язності.
Визначення 6.25. Ребро  називається міст, якщо видалення його із графа приводить до збільшення числа компонент зв’язності.
називається міст, якщо видалення його із графа приводить до збільшення числа компонент зв’язності.
Наприклад, у графі, зображеному на рис. 6.17 вершина 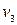 є точкою зчленування, а ребро, що з'єднує вершини
є точкою зчленування, а ребро, що з'єднує вершини 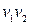 ‑ міст.
‑ міст.
Визначення 6.26. Множина ребер 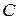 зв'язного графа
зв'язного графа  називається множиною розрізу, якщо видалення ребер із множини
називається множиною розрізу, якщо видалення ребер із множини 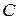 порушує зв’язність графа, а видалення власної підмножини множини
порушує зв’язність графа, а видалення власної підмножини множини 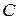 залишає граф зв'язним. Якщо множина
залишає граф зв'язним. Якщо множина 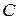 складається з одного ребра, то це ребро називається ребром розрізу.
складається з одного ребра, то це ребро називається ребром розрізу.
Приклад 6.15. Визначити ребра розрізу графа, зображеного на рис. 6.19.
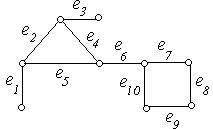
Рис. 6.19.
Рішення: р ебра 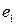 ,
, 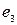 і
і 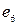 ‑ є ребрами розрізу. Їх видалення порушує зв’язність графа.
‑ є ребрами розрізу. Їх видалення порушує зв’язність графа.
Приклад 6.16. Визначити множини розрізу для графа, зображеного на рис. 6.20.
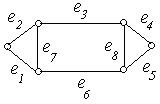
Рис. 6.20.
Рішення. Множинами розрізу для даного графа можуть бути, наприклад:
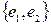 ,
, 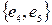 ,
, 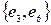 ,
, 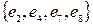 ,
, 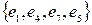 і т.д.
і т.д.
6.3.2.  ‑ орієнтований граф
‑ орієнтований граф
Визначення 6.27. Послідовність ребер, у якому кінець кожного попереднього ребра 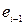 збігається з початком наступного
збігається з початком наступного 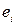 , називається шляхом або орієнтованим маршрутом. У шляху те саме ребро може зустрічатися кілька разів.
, називається шляхом або орієнтованим маршрутом. У шляху те саме ребро може зустрічатися кілька разів.
Визначення 6.28. Початком шляху є вершина 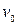 ребра
ребра 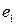 , а кінцем шляху є вершина
, а кінцем шляху є вершина 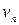 ребра
ребра 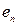 .
.
Визначення 6.29. Довжиною орієнтованого маршруту називається кількість орієнтованих ребер, що входять у цей шлях.
Приклад 6.17. Для графа, зображеного на рис. 6.21, приведемо приклади орієнтованих маршрутів з вершини 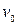 до вершини
до вершини 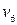 :
: 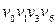 ;
; 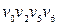 ;
; 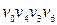 ‑ довжини 3;
‑ довжини 3; 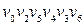 ‑ довжини 5.
‑ довжини 5.
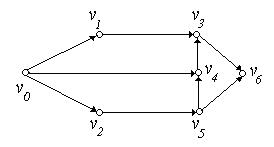
Рис. 6.21.
Визначення 6.30. Орієнтованим ланцюгом називається шлях, кожне ребро якого зустрічається не більше одного разу, і простим ланцюгом, якщо будь-яка вершина орграфа  інцидентна не більш ніж двом його ребрам.
інцидентна не більш ніж двом його ребрам.
Визначення 6.31. Контуром називається шлях, початок 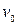 і кінець
і кінець 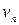 якого збігаються. Контур називається циклом, якщо він є ланцюгом, і простим циклом – якщо це простий ланцюг.
якого збігаються. Контур називається циклом, якщо він є ланцюгом, і простим циклом – якщо це простий ланцюг.
Приклад 6.18. Для графа, зображеного на рис. 6.22,а, приклади: орієнтованого ланцюга ‑ 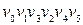 ; контуру ‑
; контуру ‑ 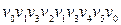 ; циклу ‑
; циклу ‑ 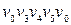 . Для графа, зображеного на рис. 6.22,б, приклади: простого орієнтованого ланцюга ‑
. Для графа, зображеного на рис. 6.22,б, приклади: простого орієнтованого ланцюга ‑ 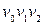 ; простого циклу ‑
; простого циклу ‑ 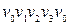 . При цьому зауважимо, що при записі циклу як для орієнтованого, так і для неорієнтованого графа, як початком, так і кінцем може бути обрана будь-яка вершина. Наприклад:
. При цьому зауважимо, що при записі циклу як для орієнтованого, так і для неорієнтованого графа, як початком, так і кінцем може бути обрана будь-яка вершина. Наприклад: 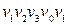 ;
; 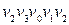 і т.п.
і т.п.
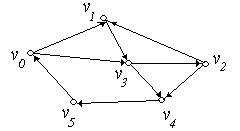
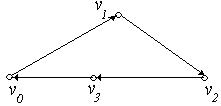
(а) (б)
Рис. 6.22.
Визначення 6.32. Для кожного орієнтованого графа  може бути побудований неорієнтований граф
може бути побудований неорієнтований граф 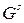 , такий, що всі вершини цих графів збігаються, а кожне ребро
, такий, що всі вершини цих графів збігаються, а кожне ребро  (крім петель), стане неорієнтованим ребром графа
(крім петель), стане неорієнтованим ребром графа 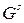 . У такому випадку граф
. У такому випадку граф 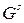 називається співвіднесеним графом орієнтованого графа
називається співвіднесеним графом орієнтованого графа  .
.
Приклад 6.19. Для графа  , зображеного на рис. 6.23,а, співвіднесений граф
, зображеного на рис. 6.23,а, співвіднесений граф 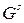 буде мати вигляд (рис. 6.23,б):
буде мати вигляд (рис. 6.23,б):
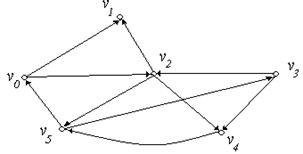
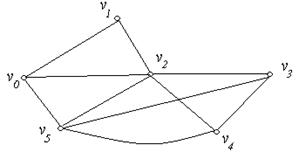
(а) (б)
Рис. 6.23.
Визначення 6.33. Вершина 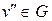 називається досяжною з вершини
називається досяжною з вершини 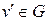 , якщо існує шлях з початком у
, якщо існує шлях з початком у 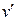 і кінцем у
і кінцем у 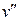 .
.
Визначення 6.34. Орієнтований граф  називається зв'язним, якщо його співвіднесений граф
називається зв'язним, якщо його співвіднесений граф 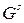 є зв'язним. Орієнтований граф називається сильно зв'язним, якщо для будь-якої пари вершин
є зв'язним. Орієнтований граф називається сильно зв'язним, якщо для будь-якої пари вершин 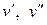 існує орієнтований шлях з
існує орієнтований шлях з 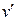 , у
, у 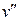 .
.
Так, наприклад, граф, зображений на рис. 6.23,а, є зв'язним, але не є сильно зв'язним.
Вправи:
1. Для неорієнтованих графів, зображених на рис. 6.24(а,б), привести приклади: маршруту; ланцюга; простого ланцюга; циклічного маршруту; циклу; простого циклу.
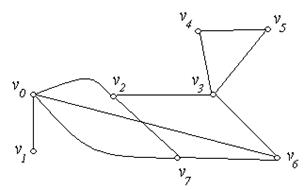
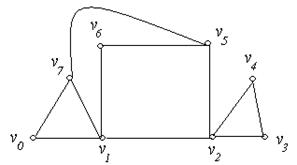
(а) (б)
Рис. 6.24.
2. Для орієнтованих графів, зображених на рис. 6.25(а,б), привести приклади: шляху; орієнтованого ланцюга; простого ланцюга; контуру; циклу; простого циклу.
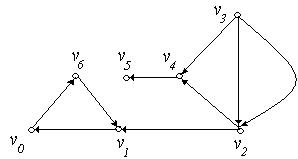
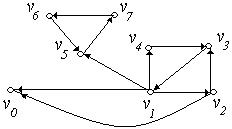
(а) (б)
Рис. 6.25.
3. Визначити число компонент зв’язності у графах  , зображених на рис. 6.26(а,б,в,г).
, зображених на рис. 6.26(а,б,в,г).
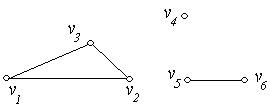
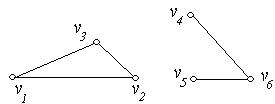
(а) (б)
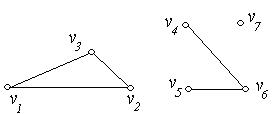
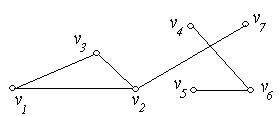
(в) (г)
Рис. 6.26.
4. Знайти на графах  , зображених на рис. 6.27 (а-г), всі точки зчленування і мости:
, зображених на рис. 6.27 (а-г), всі точки зчленування і мости:
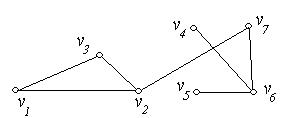
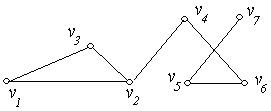
(а) (б)
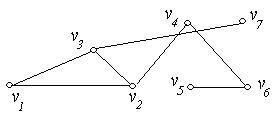
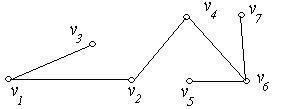
(в) (г)
Рис. 6.27.
 2015-06-28
2015-06-28 5583
5583








