Визначення 6.35. Відстанню 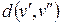 між вершинами
між вершинами 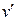 і
і 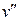 графа
графа  називається мінімальна довжина простого ланцюга з початком у вершині
називається мінімальна довжина простого ланцюга з початком у вершині 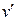 і кінцем у вершині
і кінцем у вершині 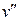 . Якщо вершини
. Якщо вершини 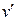 і
і 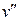 не з'єднані ланцюгом, тобто належать різним компонентам, то покладається, що
не з'єднані ланцюгом, тобто належать різним компонентам, то покладається, що 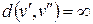 .
.
У зв'язному графі  відстань між вершинами задовольняє наступним умовам:
відстань між вершинами задовольняє наступним умовам:
1) 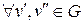 ,
, 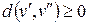 і
і 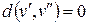 тоді і тільки тоді, коли
тоді і тільки тоді, коли 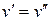 ;
;
2) 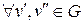 ,
, 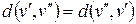 ;
;
3) 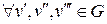 ,
, 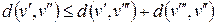 .
.
Функція 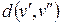 , що задовольняє трьом перерахованим умовам, називається метрикою графа.
, що задовольняє трьом перерахованим умовам, називається метрикою графа.
Визначення 6.36. Центром графа називається вершина, від якої максимальна з відстаней до інших вершин була б мінімальною.
Визначення 6.37. Периферійною точкою графа називається вершина, від якої максимальна з відстаней до інших вершин була б максимальна.
Визначення 6.38. Максимальна відстань від центра графа  до його вершин називається радіусом графа
до його вершин називається радіусом графа 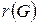 .
.
Визначення 6.39. Найпростіший ланцюг найкоротшої довжини називається геодезичним.
Визначення 6.40. Відхиленням вершини 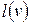 називається найбільша довжина геодезичної, яка з неї виходить.
називається найбільша довжина геодезичної, яка з неї виходить.
У зв'язку із цим можна дати ще одне визначення радіуса графа:
Визначення 6.41. Відхилення центра називається радіусом графа 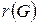 , а відхилення периферійної точки – діаметром графа
, а відхилення периферійної точки – діаметром графа 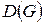 .
.
Алгоритм знаходження відстаней від даної вершини 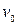 до інших вершин графа
до інших вершин графа  :
:
1) позначаємо через 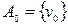 ;
;
2) позначаємо індексом 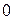 всі вершини, суміжні з вершиною
всі вершини, суміжні з вершиною 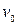 , виписуємо множину
, виписуємо множину 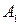 всіх цих вершин з їхніми позначками;
всіх цих вершин з їхніми позначками;
3) кожну вершину, що не належить множині 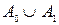 і суміжну з кожною з вершин, що належать множині
і суміжну з кожною з вершин, що належать множині 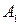 , позначаємо індексом
, позначаємо індексом 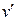 ; виписуємо множину
; виписуємо множину 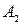 всіх цих вершин з їхніми позначками …;
всіх цих вершин з їхніми позначками …;
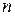 ) повторюємо описану процедуру доти, поки множина непомічених вершин не виявиться порожньою.
) повторюємо описану процедуру доти, поки множина непомічених вершин не виявиться порожньою.
Приклад 6.20. Визначити відстань від вершини 7 (для зручності запису позначимо вершини графа арабськими цифрами) до всіх вершин графа  , зображеного на рис 6.28.
, зображеного на рис 6.28.
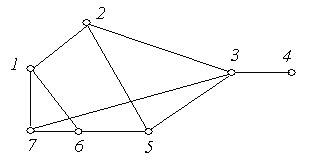
Рис. 6.28.
Рішення. Згідно алгоритму відстань від вершини 7 будемо шукати в такий спосіб:
1) 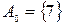 ; 2)
; 2) 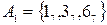 ; 3)
; 3) 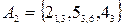 .
.
Більше непомічених вершин немає. Тобто відстані від вершини 7 до кожної з вершин графа такі:
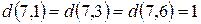 ;
; 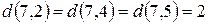 .
.
Для визначення центра і радіуса графа необхідно побудувати для нього матрицю відстаней 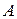 , кожен елемент якої
, кожен елемент якої 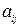 описує відстань між вершинами
описує відстань між вершинами
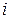 і
і 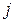 графа
графа  , тобто
, тобто 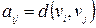 . Очевидно, що матриця відстаней
. Очевидно, що матриця відстаней 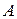
симетрична щодо головної діагоналі (елементи якої дорівнюють нулю, тому що 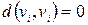 ).
).
Приклад 6.21. Визначити центр, периферійні вершини, радіус і діаметр графа  , зображеного на рис. 6.29.
, зображеного на рис. 6.29.
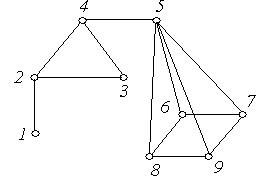
Рис. 6.29.
Рішення. Матриця відстаней графа  має вигляд.
має вигляд.
Знайдемо максимальну відстань від кожної з вершин графа 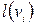 як
як 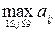 :
:
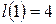 ;
; 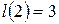 ;
; 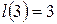 ;
; 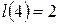 ;
; 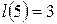 ;
; 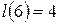 ;
; 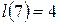 ;
; 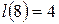 ;
; 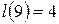 .
.
Отже, згідно з визначенням 6.36, центром графа є вершина 4; периферійні вершини – 1, 6, 7, 8, 9. Радіус графа 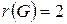 , а діаметр графа
, а діаметр графа 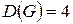 .
.
Вправи:
1. Визначити відстані від зазначеної вершини до всіх вершин графа  , зображеного на рис 6.30 (а‑ г):
, зображеного на рис 6.30 (а‑ г):
а) від вершини 5; б) від вершини 2;
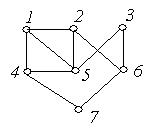
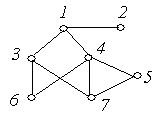
(а) (б)
в) від вершини 6; г) від вершини 3.
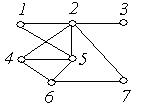
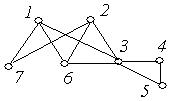
(в) (г)
Рис. 6.30.
2. Визначити центр, периферійні точки, радіус, діаметр графа  , зображеного на рис. 6.31(а,б):
, зображеного на рис. 6.31(а,б):
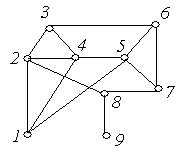
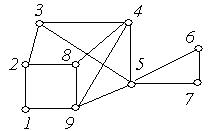
(а) (б)
Рис. 6.31.
 2015-06-28
2015-06-28 1807
1807








