Визначення 6.51. Неорієнтованим деревом (або просто деревом)називається неорієнтований зв'язний граф без циклів, отже без петель і кратних ребер, що має не менш двох вершин.
Дерево є мінімальним зв'язним графом у тому розумінні, що видалення хоча б одного ребра приводить до того, що граф виявляється незв'язним.
Приклад 6.26. Чи є графи, зображені на рис. 6.49, (а), (б) деревами?
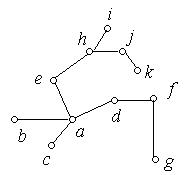
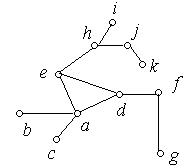
(а) (б)
Рис. 6.49.
Рішення:
Граф на рис. 6.49(а) є деревом, тому що він зв'язний і не містить циклів. Граф на рис. 6.49(б) не є деревом, тому що містить цикл 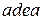 .
.
Дамо без доведення ряд теорем, корисних для вивчення дерев. Читач може довести їх самостійно.
Теорема 6.9. Будь-яке дерево  з
з 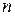 вершинами містить
вершинами містить 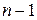 ребро.
ребро.
Теорема 6.10. Нехай  ‑ граф, що містить більше однієї вершини. Видаляючи його ребра можна одержати дерево тоді і тільки тоді, коли він зв'язний.
‑ граф, що містить більше однієї вершини. Видаляючи його ребра можна одержати дерево тоді і тільки тоді, коли він зв'язний.
Визначення 6.52. Лісом називається незв'язний неорієнтований граф без циклів. Зв'язані компоненти лісу є деревами.
Приклад 6.27. На рис. 6.50 наведений приклад лісу, що містить три дерева.
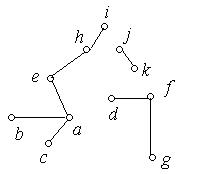
Рис. 6.50.
Добре зрозумілим прикладом дерева є: будь-яке генеалогічне дерево; організаційна структура будь-якого підприємства, організації.
Визначення 6.53. Орієнтованим деревом називається вільний від петель орієнтований граф, співвіднесений граф якого є деревом; тому якщо існує шлях від вершини v ' до вершини v '', то він єдиний.
Помітимо, що якщо в орієнтованому дереві є ребро 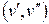 , то немає ребра
, то немає ребра 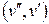 , інакше шлях
, інакше шлях 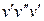 був би циклом.
був би циклом.
Приклад 6.28. На рис. 6.51 наведено приклад орієнтованого дерева:
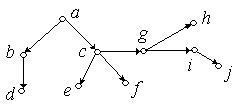
Рис. 6.51.
Визначення 6.54. Вершини дерева степіня 1 називаються листя, інші вершини – внутрішніми вершинами.
Наприклад, у дерева, зображеного на рис. 6.49(а), листя це вершини 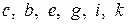 . Інші вершини є внутрішніми.
. Інші вершини є внутрішніми.
Дерева визначаються такою властивістю: для будь-яких двох вершин v ', v '' дерева 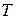 шлях з вершини v ' до вершини v '' єдиний. І, навпаки, якщо для будь-яких двох вершин v ', v '' графа
шлях з вершини v ' до вершини v '' єдиний. І, навпаки, якщо для будь-яких двох вершин v ', v '' графа  існує єдиний шлях з вершини v ' до вершини v '', тоді граф
існує єдиний шлях з вершини v ' до вершини v '', тоді граф  ‑ дерево.
‑ дерево.
Припустимо, що дерево являє собою якийсь фізичний об'єкт, рухливий у вершинах. Його можна підвісити за кожну з вершин. Так, наприклад, якщо дерево, зображене на рис. 6.49(а) підвісити за вершину  , або
, або  , то воно буде виглядати, як показано на рис. 6.52(а) або на рис 6.52 (б).
, то воно буде виглядати, як показано на рис. 6.52(а) або на рис 6.52 (б).
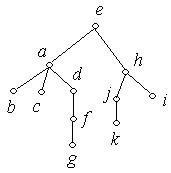
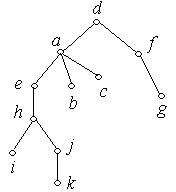
(а) (б)
Рис. 6.52.
Обрана нами вершина називається коренем дерева і розташовується в самій верхній його частині. Для дерева на рис. 6.52(а) коренем є вершина  , а для дерева на рис. 6.52(б) – вершина
, а для дерева на рис. 6.52(б) – вершина  .
.
Визначення 6.55. Дерево, корінь якого визначений, називається кореневим деревом.
Аналогічно визначається і орієнтоване кореневе дерево. При цьому варто пам'ятати, що всі його ребра орієнтуються від кореня.
При заміні кореневого неорієнтованого дерева T на кореневе орієнтоване дерево T ', говорять, що T ' є породженим кореневим деревом T.
Приклад 6.29. На рис. 6.53(а) зображене неорієнтоване кореневе дерево, а на рис. 6.53(б) – породжене їм орієнтоване кореневе дерево.
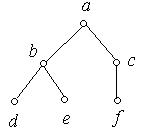
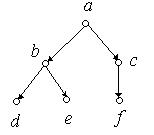
(а) (б)
Рис. 6.53.
Якщо корінь дерева обраний, то можна ввести ще ряд визначень.
Визначення 6.56. Рівнем вершини 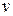 називається довжина єдиного шляху від кореня дерева до вершини
називається довжина єдиного шляху від кореня дерева до вершини 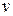 .
.
Визначення 6.57. Висотою дерева називається довжина самого довгого шляху від кореня дерева до листя.
Приклад 6.30. Для кореневого дерева, зображеного на рис. 6.54, визначити рівень вершини  , висоту дерева.
, висоту дерева.
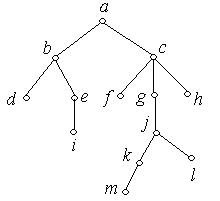
Рис. 6.54.
Рішення: Рівень вершини  дорівнює двом; а висота дерева з коренем у вершині
дорівнює двом; а висота дерева з коренем у вершині 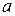 дорівнює максимальному шляху від кореня до вершини
дорівнює максимальному шляху від кореня до вершини 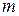 ‑
‑ 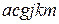 ‑дорівнює п'яти.
‑дорівнює п'яти.
Для генеалогічних дерев дамо ряд визначень. Їх можна розповсюдити на будь-які орієнтовані кореневі дерева.
Визначення 6.58. Якщо існує орієнтоване ребро з u в u, то вершина u називається батьком вершини v, а вершина v ‑ сином вершини u.
Визначення 6.59. Якщо 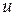 є одночасно батьком q і p, то q і p називаються братами.
є одночасно батьком q і p, то q і p називаються братами.
Визначення 6.60. Якщо існує орієнтований шлях з вершини u у вершину v, то вершина u називається предком вершини v, а вершина v ‑ нащадком вершини u.
Приклад 6.31. Визначити батьків і синів, братів, предків і нащадків кореневого орієнтованого дерева, зображеного на рис. 6.55.
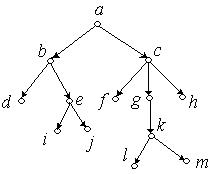
Рис. 6.55.
Рішення: 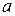 є батьком
є батьком 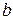 і
і  ;
; 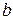 ‑ батьком
‑ батьком  і
і  ;
;  ‑ батьком
‑ батьком 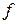 ,
, 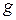 і
і 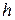 ;
;  ‑ батьком
‑ батьком 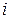 і
і 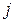 ;
; 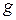 ‑ батьком
‑ батьком 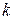 ;
; 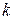 ‑ батьком
‑ батьком  і
і 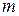 . І навпаки:
. І навпаки: 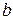 і
і  ‑ сини
‑ сини 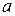 ;
;  і
і  ‑ сини
‑ сини 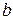 ;
; 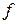 ,
, 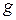 і
і 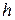 ‑ сини
‑ сини  ;
; 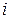 і
і 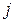 ‑ сини
‑ сини  ;
; 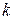 ‑ син
‑ син 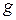 ;
;  і
і 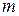 ‑ сини
‑ сини 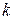 .
.
Груп нащадків і предків можна виділити дуже багато, приведемо лише деякі приклади: 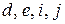 ‑ нащадки
‑ нащадки 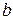 , отже,
, отже, 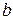 ‑ предок для
‑ предок для 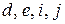 ;
;  є нащадком
є нащадком  , отже,
, отже,  ‑ предок
‑ предок  .
.
Вправи:
1. Які з наведених на рис. 6.56 (а) − (к) графів є деревами:
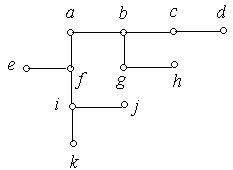
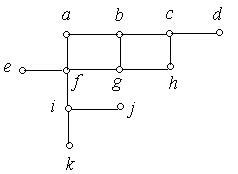
(а) (б)
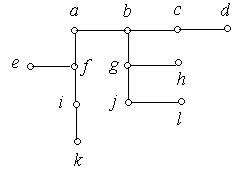
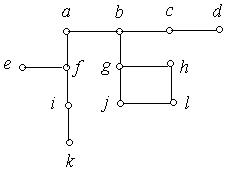
(в) (г)
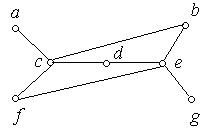
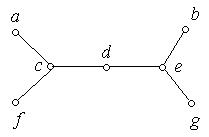
(д) (е)
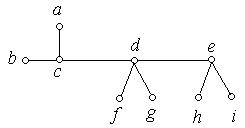
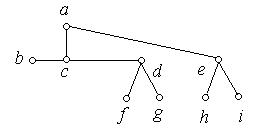
(ж) (з)
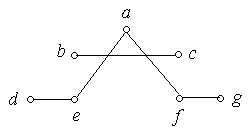
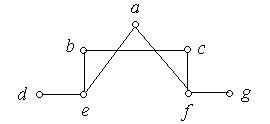
(и) (к)
Рис. 6.56.
2. Для кожного графа з попередньої вправи:
а) використати як корінь вершину  і намалювати кореневе дерево;
і намалювати кореневе дерево;
б) намалювати породжене кореневе орієнтоване дерево.
3. Для кореневих орієнтованих дерев, отриманих у завданні 2:
а) знайдіть нащадків вершини  ; б) знайдіть предків вершини
; б) знайдіть предків вершини  ;
;
в) знайдіть батька вершини 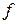 ; г) знайдіть синів вершини
; г) знайдіть синів вершини  ;
;
д) знайдіть висоту дерева; е) знайдіть рівень вершини 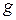 ;
;
ж) знайдіть листи дерева.
 2015-06-28
2015-06-28 1838
1838