Мы будем использовать таблицу векторного произведения единичных векторов 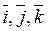 :
:
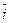 | 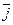 | 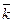 | |
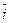 | 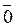 | 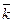 | - 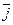 |
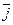 | - 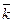 | 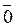 | 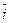 |
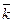 | 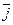 | - 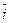 | 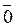 |
Чтобы не ошибиться со знаком, удобно пользоваться схемой:
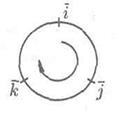
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора  = ax
= ax 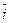 +ay
+ay 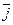 +az
+az 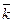 и
и  = bx
= bx 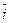 +by
+by 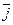 +bz
+bz 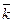 . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
. Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
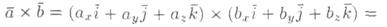
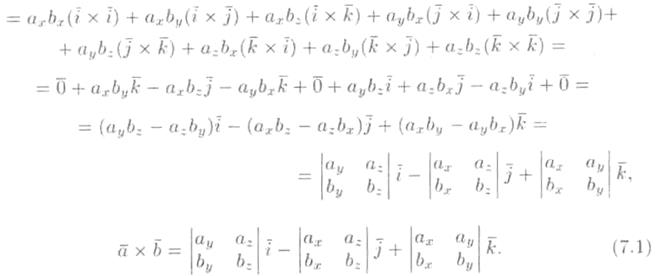
Полученную формулу можно записать еще короче:
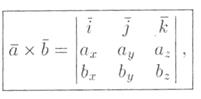
так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки. Данное равенство легко запоминается.
4. Некоторые приложения векторного произведения
 2015-06-28
2015-06-28 1720
1720
