2015-06-28
2523
1. При перестановке сомножителей векторное произведение меняет знак, т. е. 
х 
= - ( х ) (см. рис. 19).
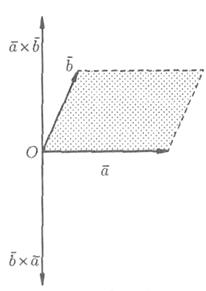
Рис. 19.
Векторы х и х коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки , , х и , , х противоположной ориентации).
Значит, х = - ( х ).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. λ( х ) = (λ ) х = х(λ ).
Пусть λ > 0. Вектор λ ( х ) перпендикулярен векторам и . Вектор (λ ) х также перпендикулярен векторам и (векторы , λ лежат в одной плоскости). Значит, векторы λ( х ) и (λ ) х коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
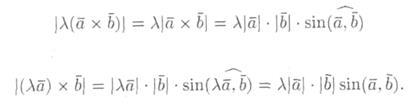
Поэтому λ( х ) и λ х .
3. Два ненулевых вектора а и В коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. || ↔ х = 0.
Если || , то угол между ними равен 0° или 180°. Но тогда | х | = | | • | | • 
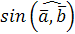= 0. Значит, х = 0.
Если же х = 0, то | | • | | sin φ = 0. Но тогда φ = 0° или φ = 180°, т. е. || .
В частности,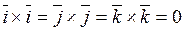 
.
4. Векторное произведение обладает распределительным свойством:
( + ) х 
= х + х .
