Векторным произведением вектора а на вектор b называется третий вектор, обозначаемый символом [ а,b ] и удовлетворяющий следующим условиям:
1. 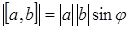 , где
, где 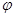 - угол между векторами а и b;
- угол между векторами а и b;
2. Вектор [ а,b ] перпендикулярен каждому из векторов а и b;
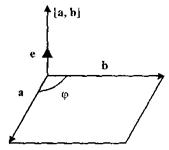
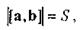 Из условия 1 следует, что модуль векторного произведения [ а,b ] равен площади S параллелограмма, построенного на векторах а и b (рис.), т.е.
Из условия 1 следует, что модуль векторного произведения [ а,b ] равен площади S параллелограмма, построенного на векторах а и b (рис.), т.е.
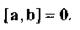 Пусть векторы а и b коллинеарны, т.е.
Пусть векторы а и b коллинеарны, т.е. 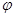 =0 или
=0 или 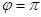 , тогда
, тогда 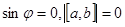 следовательно,
следовательно,
Векторное произведение двух векторов обладает свойствами:
1) антиперестановочности множителей
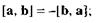
2) сочетательности относительно скалярного множителя
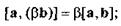
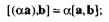
3) распределительности относительно сложения
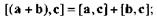
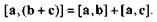
Вопрос о выражении векторного произведения через координаты перемножаемых векторов решает следующая теорема.
Теорема
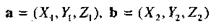 Векторное произведение [ а,b ] двух векторов
Векторное произведение [ а,b ] двух векторов
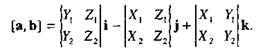 выражается формулой
выражается формулой
Следствие 1.
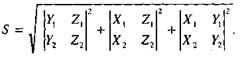 Площадь параллелограмма, построенного на векторах а и b, вычисляется по формуле
Площадь параллелограмма, построенного на векторах а и b, вычисляется по формуле
Следствие 2.
Площадь треугольника АВС определяется формулой
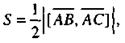
 2015-06-28
2015-06-28 612
612








