Пусть даны три вектора 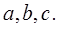 Вектор а умножим векторно на b, векторное произведение [ а,b ] умножим скалярно на с, в результате получаем число, которое называют векторно-скалярным произведением, или смешанным произведением [ а,b ] с трех векторов
Вектор а умножим векторно на b, векторное произведение [ а,b ] умножим скалярно на с, в результате получаем число, которое называют векторно-скалярным произведением, или смешанным произведением [ а,b ] с трех векторов 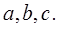
Геометрический смысл смешанного произведения трех векторов выясняет следующая теорема.
Теорема
Смешанное произведение [ а,b ] с трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах
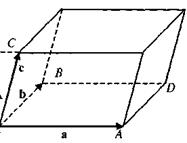
Следствие 1.
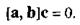 Векторы
Векторы 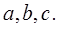 компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т. е.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т. е.
Следствие 2. Справедливо равенство [ а,b ] с = а [ b, с ].
Теорема. Смешанное произведение трех векторов
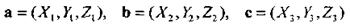
определяется формулой
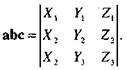
 2015-06-28
2015-06-28 503
503








