Пусть в декартовой прямоугольной системе координат в пространстве даны две точки 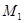 и
и 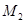 , заданные своими координатами
, заданные своими координатами 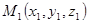 и
и 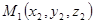 . Тогда координаты вектора
. Тогда координаты вектора 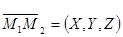 в этой системе координат определяются по формулам:
в этой системе координат определяются по формулам:
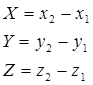
Если вектор а имеет координаты X, Y, Z, то он может быть представлен в виде 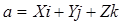 , где
, где 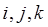 - единичные векторы координатных осей (называемые ортами). Такое представление вектора а называется разложением вектора а по базисным векторам
- единичные векторы координатных осей (называемые ортами). Такое представление вектора а называется разложением вектора а по базисным векторам 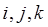 .
.
Длина вектора а, заданного своими координатами выражается формулой: 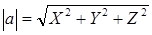
Пусть векторы а и b заданны своими координатами 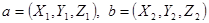 , тогда координаты векторов
, тогда координаты векторов 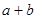 ,
, 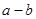 ,
, 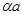 выражаются формулами:
выражаются формулами:
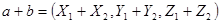
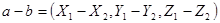
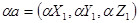
Необходимое и достаточное условие коллинеарности двух векторов 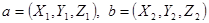 выражается формулой:
выражается формулой:
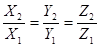 .
.
 2015-06-28
2015-06-28 2433
2433
