Определение 9 (Правило треугольника).
Суммой векторов 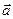 и
и 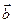 , отложенных последовательно, называется вектор
, отложенных последовательно, называется вектор 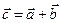 , начало которого совпадает с началом первого слагаемого вектора, а конец – с концом второго.
, начало которого совпадает с началом первого слагаемого вектора, а конец – с концом второго.
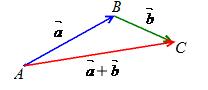
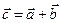 ,
,
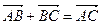 (7.1)
(7.1)
Сумма векторов существует и определена однозначно.
Свойства сложения:
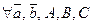
| 1. | С=В | 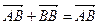 | 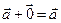 |
| 2. | С=В, В=А | 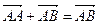 | 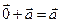 |
| 3. | С=А | 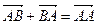 | 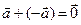 |
| 4. | Коммутативность | 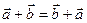 | |
| 5. | Ассоциативность | 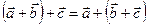 |
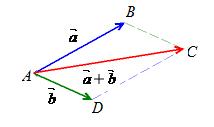
Определение 10 (Правило параллелограмма).
Суммой векторов 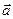 и
и 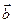 , отложенных от общего начала, называется вектор
, отложенных от общего начала, называется вектор 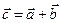 , задаваемый диагональю построенного на них, как на сторонах, параллелограмма, исходящей из их общего начала. Начало вектора суммы совпадает с началом слагаемых векторов, а конец – с противоположным концом диагонали параллелограмма.
, задаваемый диагональю построенного на них, как на сторонах, параллелограмма, исходящей из их общего начала. Начало вектора суммы совпадает с началом слагаемых векторов, а конец – с противоположным концом диагонали параллелограмма.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух связных (фиксированных) векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Определение 11 (Правило многоугольника).
Суммой nвекторов 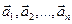 , отложенных последовательно, называется вектор
, отложенных последовательно, называется вектор 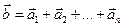 , начало которого совпадает с началом первого слагаемого вектора
, начало которого совпадает с началом первого слагаемого вектора 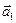 , а конец – с концом последнего слагаемого вектора
, а конец – с концом последнего слагаемого вектора 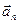 .
.
 2015-06-28
2015-06-28 1757
1757
