Из определения следует:
1) 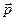 ||
||  ,
,
2) если  =
= 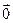 , то
, то 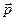 = a
= a 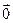 =
= 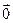 ;
;
3) если a =0, то 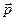 =0×
=0×  =
= 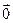 .
.
Для произвольных чисел a, b и векторов  и
и 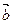 справедливы следующие равенства:
справедливы следующие равенства:
4) 1×  =
=  ; 6)
; 6) 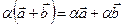
5) 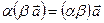 7)
7) 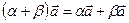
Для доказательства достаточно рассмотреть выполнение условий определения.
Для примера докажем свойства 4-5.
4) 1×  =
= 
| Условия определения | |
| 1. Длина | 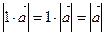 |
| 2. Направление | 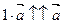 , так как 1>0. , так как 1>0. |
| Вывод | 1×  = =  . . |
5) 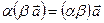
| Условия определения | Слева 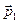 | Справа 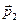 | Вывод |
| 1. Длина | 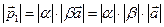 | 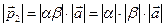 | |  |=| |=|  | | |
2.0) Если 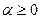 и/или и/или 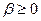 | |||
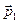 = = 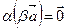 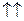  | 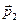 = = 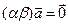 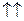  | 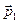 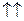 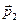 | |
| 2. Направление | 2.1) Если 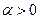 и и 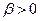 , , | ||
то 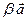 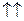  и и 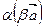 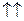  , т.е. , т.е. 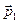 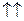  . . | то 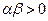 и и 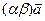 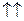  , т.е. , т.е. 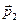 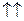  . . | 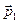 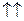 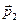 | |
2.2) Если 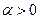 и и 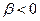 , , | |||
то 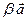 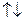  и и 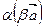 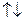  , т.е. , т.е. 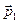 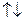  . . | то 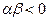 и и 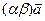 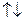  , т.е. , т.е. 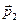 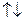  . . | 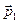 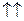 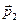 | |
2.3) Если 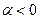 и и 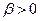 , , | |||
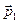 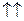 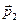 | |||
2.4) Если 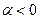 и и 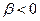 , , | |||
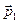 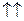 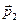 | |||
| Вывод | Так как 1) | 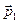 |=| |=| 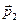 |; 2) |; 2) 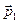 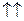 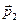 , то , то 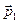 = = 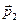 , т.е. , т.е. 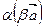 = = 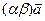 . . |
пп. 2.3 и п.2.4 заполните самостоятельно. Докажите остальные свойства.
 2015-06-28
2015-06-28 1042
1042








