Вычитание векторов

Разность векторов существует и определена однозначно. Вычитание вводится как операция, обратная сложению.

Определение 12.

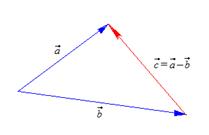
Разностью векторов 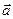и 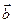, отложенных от общего начала, называется вектор 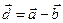, начало которого совпадает с концом вычитаемого вектора, а конец – с концом уменьшаемого вектора.

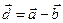, если .

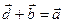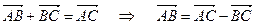. (7.2)

Для любых двух векторов и : – = +(– ).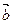

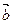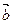Определение 12*.

Разностью двух векторов 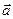и 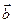, называют третий вектор, равный сумме уменьшаемого вектора 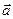и вектора (– 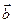), противоположного вычитаемому.

Это определение указывает правило построения разности векторов.