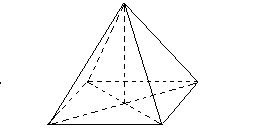
и плоскостью основания АВС является линейный угол SЕА. В основании данной правильной пирамиды – квадрат АВСD. Значит, ВD=АС=8, тогда ОС = 8:2 = 4. Рассмотрим ΔSЕО – прямоугольный, т.к. SО = 9 - высота данной пирамиды. По условию точки K и M – середины рёбер СD и BС соответственно, значит, ОЕ = ОС:2 = 4:2 = 2. tg |
 Пример 7.
Пример 7.
| Задания 12.Диагональ АС основания правильной четырехугольной пирамиды SABCD равна 6. Высота пирамиды равна 4. Найдите длину бокового ребра SB. | ||
| S D C O А B | 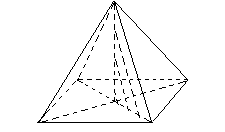  Решение:
В основании данной правильной пирамиды – квадрат ABCD. Значит, по свойствам квадрата АС=BD, ОВ= BD:2=6:2=3.
SO-высота пирамиды, значит, Решение:
В основании данной правильной пирамиды – квадрат ABCD. Значит, по свойствам квадрата АС=BD, ОВ= BD:2=6:2=3.
SO-высота пирамиды, значит,
 ОSB - прямоугольный.
По теореме Пифагора
SВ2 = SО2 + ОB2, тогда ОSB - прямоугольный.
По теореме Пифагора
SВ2 = SО2 + ОB2, тогда
| S D C O А B |
SВ2 = 42 + 32, SВ2 = 16 + 9, SВ2 = 25,
т.к. SВ  0, тогда длина бокового ребра SВ = 5.
В бланк ответов: 5 0, тогда длина бокового ребра SВ = 5.
В бланк ответов: 5
|
 2015-06-24
2015-06-24 400
400

 S
D К
А О
С
М
В
S
D К
А О
С
М
В
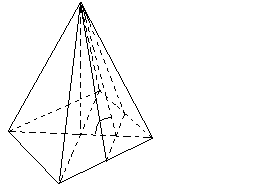 S
D
К
А О
Е С
М
В
S
D
К
А О
Е С
М
В
 SЕА =tg
SЕА =tg 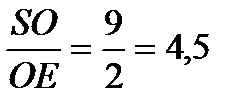 . В бланк ответов: 4,5
. В бланк ответов: 4,5






