Мы выяснили, что на множестве векторов (обозначим его V 3) трехмерного пространства выполняются свойств линейных операций, а именно: " 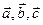 " a, b Î R
" a, b Î R
1. 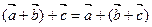 5.
5. 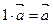
2. 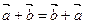 6.
6. 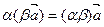
3. $ 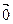 /
/ 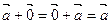 7.
7. 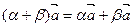
4. $–  /
/ 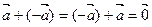 8.
8. 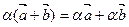 (7.4)
(7.4)
Говорят, что множество векторов V 3 образует векторное пространство над полем R, в котором определено сложение векторов, умножение вектора на действительное число, удовлетворяющее свойствам 1–8, называемым системой аксиом векторного пространства.
Векторное пространство называется n - мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n +1 векторов линейно зависима.
Обозначается: n =dim V или Vn.
Подмножество L векторного пространства V 3 образует векторное подпространство, если оно само образует векторное пространство и удовлетворяет условиям:
1) 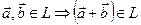 , 2)
, 2) 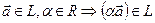 . (7.5)
. (7.5)
 2015-06-28
2015-06-28 589
589








