Анализ динамики экономических показателей основан на сравнении уровней ряда между собой за разные (отчетный и базисный) периоды времени. Отчетный (текущий) период времени – это период времени, показатель за который сравнивается с показателем за другой период времени. Базисный (сравниваемый) период времени – это период времени,показатель за который является базой сравнения. Если сравниваются два уровня ряда за последовательные периоды времени 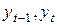 , то показатель сравнения называется цепным. Если сравниваются уровни ряда
, то показатель сравнения называется цепным. Если сравниваются уровни ряда 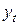 с каким-нибудь одним уровнем, время которого не меняется
с каким-нибудь одним уровнем, время которого не меняется 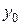 , то полученный показатель сравнения называется базисным. В качестве базисного уровня может использоваться любой уровень ряда. Однако, как правило, в качестве базисного уровня используется первый уровень ряда
, то полученный показатель сравнения называется базисным. В качестве базисного уровня может использоваться любой уровень ряда. Однако, как правило, в качестве базисного уровня используется первый уровень ряда 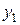 .
.
Рассмотрим основные аналитические показатели, используемые при анализе динамики экономических показателей. В качестве иллюстрации расчета аналитических показателей используем данные следующего временного ряда:
| y1 | y2 | y3 | y4 | y5 | y6 | y7 |
Абсолютный прирост Δ показывает на сколько уровень ряда в отчетном периоде изменился по сравнению с базисным. Абсолютный прирост бывает цепным или базисным.
Цепной абсолютный прирост
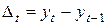 ; (8.2)
; (8.2)
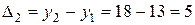 ;
; 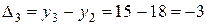 , и т.д.
, и т.д.
Базисный абсолютный прирост
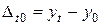 . (8.3)
. (8.3)
Для расчета за базисный уровень примем значение первого уровня ряда у 1
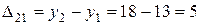 ;
; 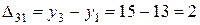 и т.д.
и т.д.
Цепные и базисные абсолютные приросты связаны между собой следующим образом:
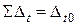 . (8.4)
. (8.4)
По известным величинам с помощью уравнения (8.4) можно найти неизвестные. Так, несколько последовательных цепных абсолютных приростов можно заменить одним базисным, например, 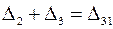 ; 5+(−3)=2. Зная несколько последовательных базисных абсолютных приростов, можно найти цепные абсолютные приросты. Например,
; 5+(−3)=2. Зная несколько последовательных базисных абсолютных приростов, можно найти цепные абсолютные приросты. Например, 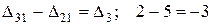 .
.
Темп роста Тр показывает во сколько разв долях или процентах уровень ряда в отчетном периоде времени изменился по сравнению с базисным. Темп роста может быть цепным или базисным.
Цепной темп роста
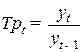 . (8.5)
. (8.5)
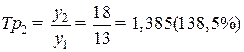 ;
; 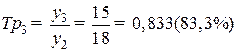 .
.
Базисный темп роста
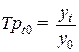 . (8.6)
. (8.6)
Для расчета за базисный уровень примем значение первого уровня ряда у 1
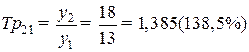 ;
; 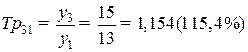 .
.
Цепные и базисные темпы роста связаны между собой следующим образом
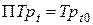 . (8.7)
. (8.7)
С помощью уравнения (8.7) можно, например, несколько последовательных цепных темпов роста заменить базисным:
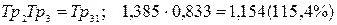 .
.
Кроме того, разделив два базисных темпа роста, можно найти один цепной или произведение нескольких цепных темпов роста:
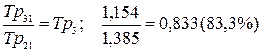 .
.
Темп прироста Тпр показывает, на сколько в долях или процентах уровень ряда в отчетном периоде времени изменился по сравнению с базисным. Темп прироста может быть цепным или базисным.
Цепной темп прироста
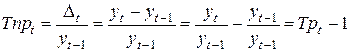 ; (8.8)
; (8.8)
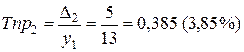 , или
, или 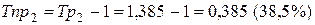 .
.
Базисный темп прироста
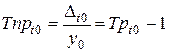 . (8.9)
. (8.9)
Для расчета за базисный уровень примем значение первого уровня ряда у 1
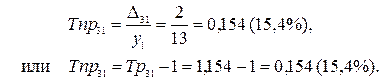
Абсолютное значение одного процента прироста |%| t показывает ,чему равен один процент прироста уровня ряда в отчетном периоде. Показатель абсолютного значения одного процента прироста бывает только цепным
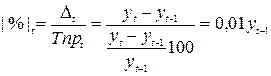 ; (8.10)
; (8.10)
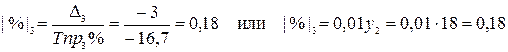 .
.
Расчет показывает, что в отчетном периоде каждый процент прироста равен 0,18 единицам абсолютного прироста уровня ряда в отчетном периоде, либо каждый процент прироста уровня ряда в отчетном периоде времени равен 0,01 уровня ряда предыдущего периода времени.
Формула (8.10) позволяет поводить промежуточные расчеты, если из трех компонентов неизвестен какой-то один.
 2015-06-28
2015-06-28 6641
6641