Сезонные колебания: понятие, анализ

Временные ряды наряду с трендом и случайностью могут содержать и сезонные колебания. Они определяются действием сезонного фактора, т.е. сменой времен года и потому проявляются в рамках одного года. Многие показатели, особенно в легкой промышленности, сельском хозяйстве, транспорте, коммунальном хозяйстве подвержены сезонной колеблемости. Это вызывает необходимость учитывать данный фактор при решении многих практических задач во многих отраслях промышленности, том числе и в текстильной промышленности. В число таких задач входят задачи планирования и прогнозирования производства продукции, анализа конъюнктуры рынка, спроса и предложения, создания необходимых материальных запасов, движения цен и т.д.

Чтобы выявить и изучить сезонные колебания во временном ряде, целесообразно провести ряд последовательных действий.

1.Изучить сущность экономического процесса, который описан с помощью временного ряда, и определить, могут ли в данном экономическом процессе иметь место колебания с периодичностью в один год, которые обусловлены изменением времени года.

2.Сформировать временной ряд, который содержал бы данные минимум за 3…5 лет. Отсутствие данных в таком объеме не позволит не только определить наличие сезонного колебания во временном ряде, но и, что самое главное, рассчитать обоснованные показатели при планировании и прогнозировании.

3.По данным сформированного временного ряда построить его графическую модель. Провести визуальный анализ графической модели с целью выявления наличия сезонного цикла.

4.После установления наличия сезонного цикла необходимо визуально оценить наличие тренда. Если в ряде тренд отсутствует или он незначителен, то сезонный цикл анализируется методом простых средних относительно среднего уровня ряда. Если тренд присутствует, то сезонный цикл анализируется относительно тренда.

Проведем анализ сезонного цикла временного ряда при условии, что в нем отсутствует тренд.

Пусть нам дан временной ряд, который содержит данные за n лет, а каждый год содержит m временных периодов (месяцев, кварталов)

,

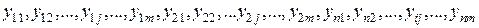где 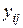– уровень ряда за i -й год и за j -й временной период (месяц, квартал).

Вначале определим среднюю временного ряда с помощью средней арифметической простой

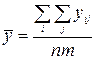. (8.29)

Потом для каждого временного периода (месяца или квартала) по всем годам рассчитаем его среднее значение

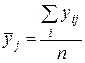. (8.30)

В итоге определим индекс сезонности для каждого временного периода (месяца, квартала), %,

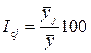. (8.31)

На основе индексов сезонности строится график сезонности временного ряда. Для этого на оси абсцисс откладывается время, а на оси ординат – индексы сезонности. Одновременно на графике проводится линия, соответствующая 100%. Она будет параллельна оси абсцисс.

Степень сезонной колеблемости может быть оценена сезонным стандартным отклонением, %,

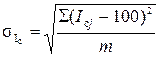. (8.32)

Данный показатель позволяет сопоставить между собой сезонную колеблемость в разных временных рядах.

Пример 8.15. Фабрика "Вымпел" в 2000, 2001, 2002 годах имела оборот, который приведен в табл.8.9. Основную номенклатуру составляли товары, имеющие сезонный спрос. Проведем анализ товарооборота с точки зрения наличия сезонных колебаний.

1.Анализ данных, приведенных в табл.8.9, показывает значительную колеблемость оборота по месяцам. Сами товары по своим потребительским свойствам больше реализуются в летние месяцы и меньше – в зимние. Это позволяет предположить, что товарооборот может иметь сезонные колебания.

Таблица 8.9

Месяц	Оборот, млн.руб.	Средний оборот за месяц	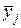Месячный сезонный индекс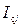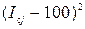
2000г.	2001г.	2002г.
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь				600,0 670,7 982,3 1194,3 1454,0 1513,0 1626,0 1365,3 938,3 730,3 675,3 658,7	58,0 64,9 95,0 115,5 140,6 146,3 157,2 132,0 90,7 70,6 65,3 63,7	1764,0 1232,0 25,0 240,3 1648,4 2143,7 3283,3 1024,0 86,5 864,4 1204,1 1317,7
Итого	–	–	–	–	–	14833,4

2. По данным табл. 8.9 построим графическую модель временного ряда

(рис.8.3) и проведем ее анализ.

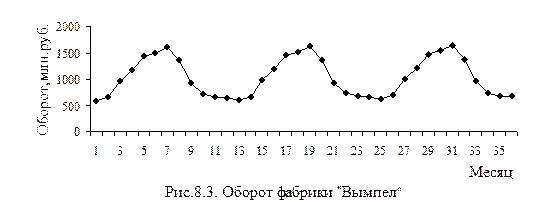
Анализ графической модели временного ряда и данных табл.8.9 показывает, что изменение данных временного ряда, несмотря на месячные колебания, в течение каждого года имеет постоянный характер, т.е. с января по июль оборот возрастает, а потом уменьшается, и эти изменения из года в год постоянны. Анализ позволяет сделать вывод о наличии во временном ряде сезонной колеблемости. На основе визуального анализа графика можно сделать и другой вывод: во временном ряде нет явной тенденции роста или уменьшения товарооборота по годам.

Рассчитаем среднюю временного ряда с помощью средней арифметической простой по формуле (8.29):

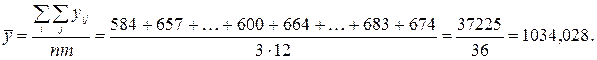
Затем по каждому месяцу за три года определим среднемесячный товарооборот по формуле (8.30), а результаты занесем в графу 5 табл. 8.9. Среднемесячный оборот в январе

.

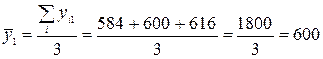Аналогичным образом рассчитаем средний товарооборот по остальным месяцам. Теперь рассчитаем индекс сезонности для каждого месяца по формуле 8.31, а результат занесем в графу 6 табл.8.9. Так, индекс сезонности за январь

.

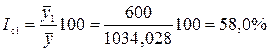Аналогичным образом рассчитаем индекс сезонности за другие месяцы. По рассчитанным индексам сезонности построим график сезонной колеблемости или сезонной волны (рис.8.4).

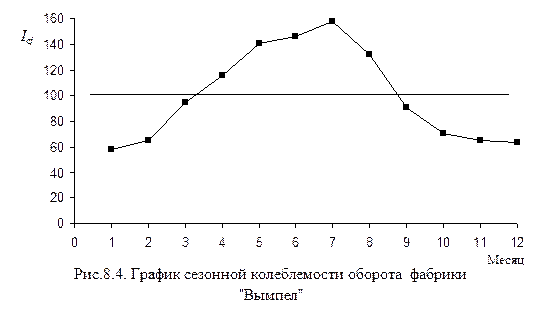
График сезонной колеблемости показывает, как в среднем в течение года изменяется товарооборот фабрики. Так, с января (1) по июль (7) товарооборот постепенно нарастает, с июля до сентября (9) резко падает, а с октября (10) до декабря (12) включительно постепенно снижается.

Сезонная колеблемость товарооборота отражает спрос на продукцию фабрики. Это позволяет оптимизировать загрузку оборудования, периодичность его ремонта, оценить потребность в рабочей силе, исходном сырье, определить оптимальную потребность в оборотных средствах и т.д.

В заключение определим степень сезонной колеблемости по формуле (8.32) и данным графы 7 табл.8.9

.

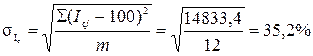Анализ сезонного цикла при условии, что во временном ряде присутствует тренд, проводится в той же последовательности, что и при анализе сезонного цикла без наличия тренда. Однако расчет ведется не от средней временного ряда, а от данных, рассчитанных по уравнению тренда.

.

Контрольные вопросы и задания

1.Что такое временной ряд,из каких элементов он состоит? Приведите примеры экономических показателей, которые вы используете в виде временных рядов в своей практической деятельности.

2. Объем незавершенного производства на начало первой декады месяца составил 90% от плана, на начало второй декады– 95%, на начало третьей декады – 100%. Определите, какой здесь используется временной ряд: интервальный или моментный?

3. Почему во временных рядах может возникнуть несопоставимость данных? Чем это может обернуться? Какие методы вы знаете для приведения уровней ряда в сопоставимый вид?

4. Имеются следующие данные

y1	y2	y3	y4	y5	y6	y7

Рассчитайте по ним все основные показатели временного ряда.

5. Постройте графики по данным табл. 8.4 и визуально оцените наличие тенденции в среднем.

6. Что такое тенденция, в каких формах она может проявляться? Приведите примеры из вашей практической деятельности. Может ли временной ряд не иметь тенденции?

7. По данным временного ряда

y1	y2	y3	y4	y5	y6	y7

определите наличие тенденции, возможный тип трендовой модели, рассчитайте ее параметры.

8. Данные табл.8.9 по месяцам преобразуйте в квартальные и проведите анализ их сезонного колебания.